标签:变长数组 限制 模型 希尔排序 维护 完全二叉树 fir change 轨迹
集合性质的数据类型离不开插入删除这两操作,主要区别就在于删除的时候删哪个,像栈删最晚插入的,队列删最早插入的,随机队列就随便删,而优先队列删除当前集合里最大(或最小)的元素。优先队列有很多应用,举几个见过的像:数据压缩的哈夫曼编码、图搜索中的 Dijkstra 算法和 Prim 算法、人工智能里的 A* 算法等,优先队列是这些算法的重要组成部分。

先来个简单的 API,应用例子是从 N 个输入里找到前 M 个大的元素,其中 N 的数目很大。因为 N 很大,没有足够的空间来存储,所以不能全部排序后输出前 M 个。得用优先队列,保留 M 个,插入超过 M 就删除最小的。
像栈和队列那样的初级优先队列实现,内部存储又可以分为有序和无序两种,有序的插入操作是 N 级别,删除是常数级别,而无序相反,所以在时间上也不尽人意。下节介绍的二叉堆实现都是 NlgM 级别,这里先蛮贴一个初级实现。
public class UnorderedMaxPQ<Key extends Comparable<Key>> {
private Key[] pq; // pq[i] = ith element on pq
private int N; // number of elements on pq
public UnorderedMaxPQ(int capacity) {
pq = (Key[]) new Comparable[capacity];
}
public boolean isEmpty() {
return N == 0;
}
public void insert(Key x) {
pq[N++] = x;
}
public Key delMax() {
int max = 0;
for (int i = 0; i < N; i++)
if (less(max, i)) max = i;
exch(max, N-1);
return pq[--N];
}
}二叉树就是节点最多有两个孩子的树,其中完全二叉树除了底层可能右边空外都是满的,二叉堆是用数组表示的符合堆顺序(heap-ordered)的完全二叉树,例:
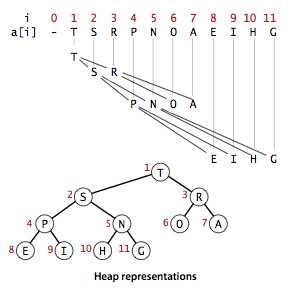
堆顺序大概就是指父母节点的值不比孩子小,然后一层一层从左到右放数组里。另外,数组从下标 1 开始,这样就可以很方便的在堆里上下移动:下标为 k 的节点的父母下标为 k/2,孩子是 2k 和 2k+1,完全不需要其它显式的连接。
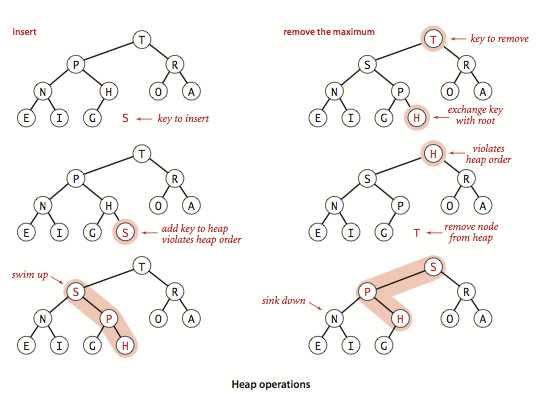
二叉堆实现的优先队列,内部存储用的是数组,插入和删除都和数组最后一个元素打交道,比较方便:插入先直接插入末尾,删除也是把 a[1] 先和末尾交换再直接删除末尾。于是乎,我们需要上浮(swim)和下沉(sink)操作,来恢复插入删除中被破坏的堆顺序。
private void swim(int k) {
while (k > 1 && less(k/2, k)) {
exch(k, k/2);
k = k/2;
}
}当孩子节点的值比父母大时,为了维护堆顺序,这个值该上浮,于是和父母的值交换,继续这一过程浮到合适的位置。所以,把元素插入到末尾之后,就给它来个上浮,安排到合适位置。
public void insert(Key x) {
pq[++N] = x;
swim(N);
}private void sink(int k) {
while (2*k <= N) {
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}当父母节点的值比孩子小时,这个节点该下沉来维护堆顺序,选两个孩子(如果有两)中较大的交换值,继续这一过程直到沉到合适的位置。于是,当删除元素时,把 a[1] 和末尾交换后删除末尾,现在的 a[1] 用下沉来找到该有的位置。
public Key delMax() {
Key max = pq[1];
exch(1, N--);
sink(1);
pq[N+1] = null;
return max;
}因为有 N 个点的完全二叉树的高度为 lgN 取下整(高度只有在节点数为 2 的幂时才会加一),所以上浮和下沉的复杂度都是 lgN 级别。
图例:
代码:
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq;
private int N;
public MaxPQ(int capacity) {
pq = (key[]) new Comparable[capacity+1];
}
public boolean isEmpty() {
return N == 0;
}
public void insert(Key key)
public Key delMax() {
/* see previous code */
}
private void swim(int k)
private void sink(int k) {
/* see previous code */
}
private boolean less(int i, int j) {
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i, int j) {
Key t = pq[i];
pq[i] = pq[j];
pq[j] = t;
}
}此外,还有一些可以考虑的,如把键设为不可变的(immutable),当它们在优先队列里的时候,客户端程序不能改变它们;内部使用变长数组;改成删除最小元素;支持随机删除和改变优先级(这个后面好像会有)等。
关于不可变多说了点,Java 里用关键字 final 就好,像 String、Integer、Double、Vector 等都是不可变的,而 StringBUilder、Stack、Java array 等是可变的。不可变数据创建之后就不能改变,这有很多好处:方便 debug,利于防范恶意代码,可以放心地作为优先队列或符号表的键等,虽然每个值都要新建,但还是利大于弊。反正,了解下啦。
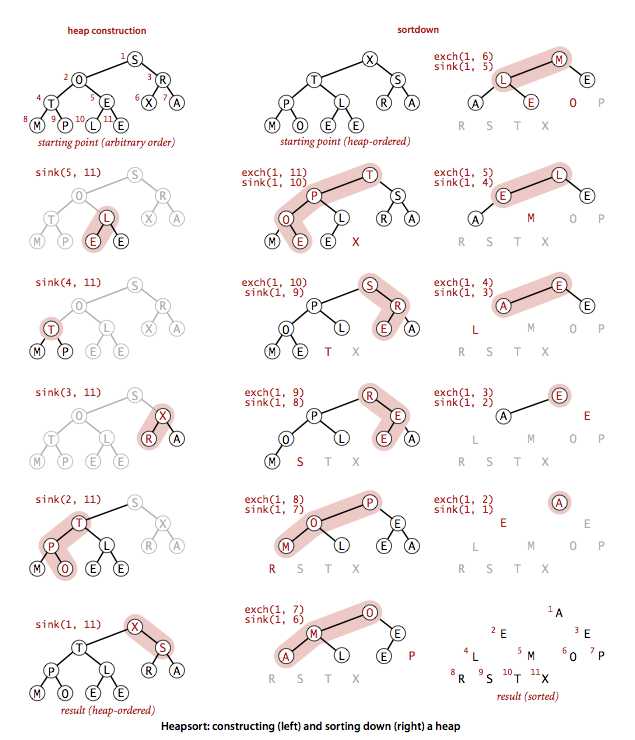
如果把数组塞进优先队列,再一个个删掉,那实际上按删掉的顺序就对数组排了个序,所以又有种全新的排序算法,叫做堆排序。这个算法自然地分成两步:先把数组调整成符合堆顺序,即构造堆,然后每次把 a[1] 和 a[N--] 交换,当 N 减到 1 时也就排好了序。另外,数组下标从 0 开始,而堆是从 1 开始,需要一定转换,下面先假设待排数组也是从 1 开始,方便说明。
对有孩子的节点用下沉操作,自底向上地构造堆。完全二叉树有孩子的节点,从 N/2 开始到 1,只要遍历一半数组。
for (int k = N/2; k >= 1; k--)
sink(a, k, N);有了堆,那排序比优先队列出队还简单:
while (N > 1) {
exch(a, 1, N--);
sink(a, 1, N);
}构造和排序的图例:
代码:
public class Heap {
public static void sort(Comparable[] pq) {
int n = pq.length;
for (int k = n/2; k >= 1; k--)
sink(pq, k, n);
while (n > 1) {
exch(pq, 1, n--);
sink(pq, 1, n);
}
}
public static void sink(Comparable[] pq, int k, int n) {
while (2*k <= n) {
int j = 2*k;
if (j < n && less(pq, j, j+1)) j++;
if (!less(pq, k, j)) break;
exch(pq, k, j);
k = j;
}
}
private static boolean less(Comparable[] pq, int i, int j) {
return pq[i-1].compareTo(pq[j-1]) < 0;
}
private static void exch(Object[] pq, int i, int j) {
Object swap = pq[i-1];
pq[i-1] = pq[j-1];
pq[j-1] = swap;
}
}可以看到,数组下标的转换也就是方法 less() 和 exch() 里索引减一。
再来张排序轨迹示例:
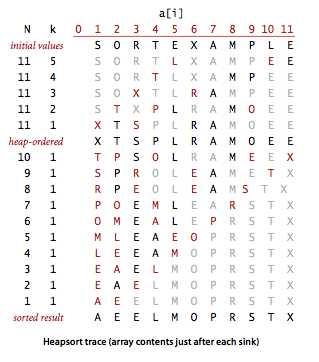
一开始调整堆顺序看不出什么,后面就有点像选择排序了,每次找出最大的放尾巴,但是需要的比较次数少得多。
构造堆的时候,复杂度甚至是 N 级别的,需要的交换次数少于 N,于是需要的比较的次数少于 2N(两个孩子的话多比较一次孩子大小),可以这样理解:
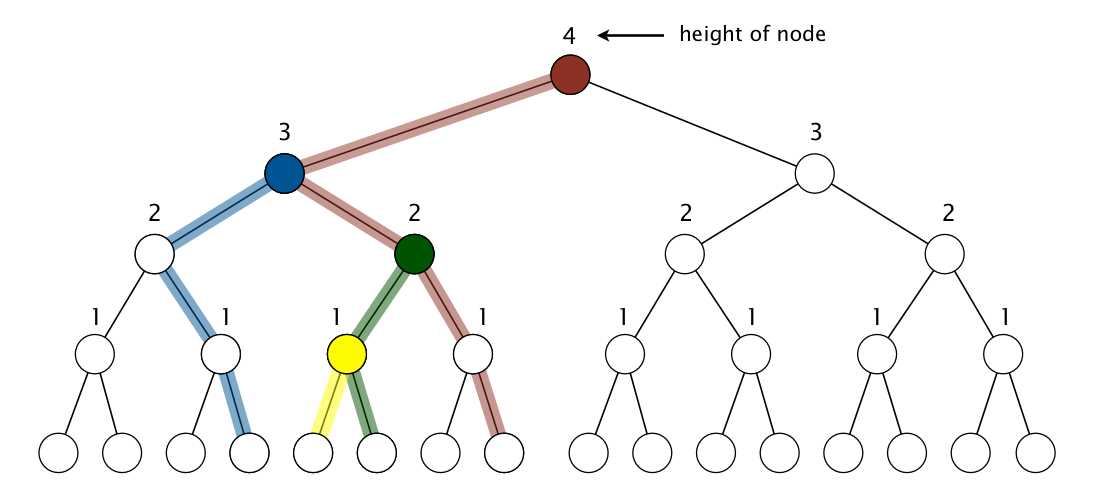
首先,n 个点的二叉堆有 n-1 条链接,因为除了根节点每个点都有条链接指向其父节点。然后,我们从点出发,按左-右-右-右-... 的顺序分配这些链接,这样链接只会属于一个点,甚至根左边那条还没点管,看上图感受下。最后,点下沉需要最多的交换次数等于属于它的链接数,所以构造时总共需要的交换次数不会超过 n。
来自 booksite 练习的最后一题。
20.Prove that sink-based heap construction uses at most 2n compares and at most n exchanges.
至于后面的排序,要遍历数组,下沉最多是树高为 lgN,显然是 NlgN 级别。于是乎,好像有了个很厉害的算法,不像归并排序需要额外的空间,不像快排最坏情况不能保证 NlgN 的性能,但现代系统的很多应用并不使用堆排序,因为它无法有效地利用缓存(cache)。数组元素很少和相邻的其它元素进行比较,因此缓存未命中的次数要远远高于大多数比较都在相邻元素间进行的算法,如快排、归并排序,甚至是希尔排序。另外,堆排序也不是稳定的。
介绍了一个借助优先队列实现的刚性球体碰撞的模拟系统,刚性球体模型有以下特点:
是个理想模型,在既与宏观现象(温度、压力)有关又和微观现象(单个原子和分子的运动)有关的统计力学中十分重要。
用计算机模拟符合这个模型的碰撞系统,其实也就是要知道每个时刻所有粒子的位置和速度,自然地想到时间驱动的解决策略:给定时间 t 时所有粒子的位置和速度,借此算出 经过时间 dt 后粒子的位置,检查是否有发生碰撞,有就回退到碰撞的时间并考虑碰撞的影响。但这样的花费太大,每个粒子检查是否有碰撞就达到了 \(N^{2}\) 级别。另外,dt 也不好把握,太大会错过很多碰撞,太小计算成本太高。于是乎,我们来考虑另外一种事件驱动的策略。
事件是未来某个时间的一次潜在碰撞,关联的优先级就是发生的时间,可以用一个优先队列来记录所有事件,快速获取下一次潜在的碰撞。碰撞预测需要些高中物理知识(继重造线代后居然是物理吗),首先,粒子和墙的碰撞相对简单:
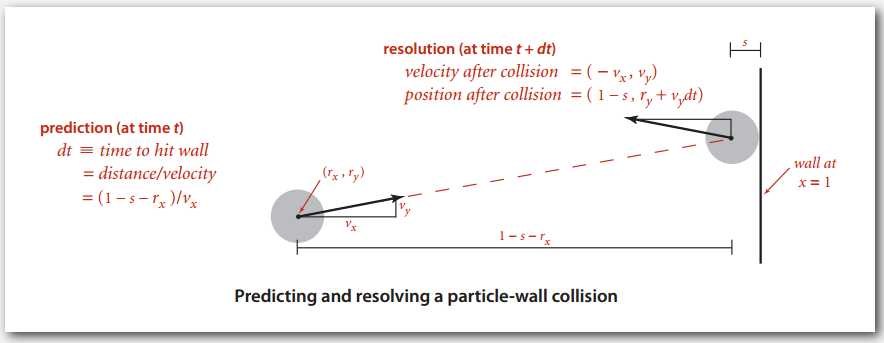
这里的单元格是边长为 1 的正方形,和其它墙的碰撞类似,不提。
粒子和粒子间的碰撞事件的发生时间比较复杂(这里不考虑多个粒子同时碰撞的情况):
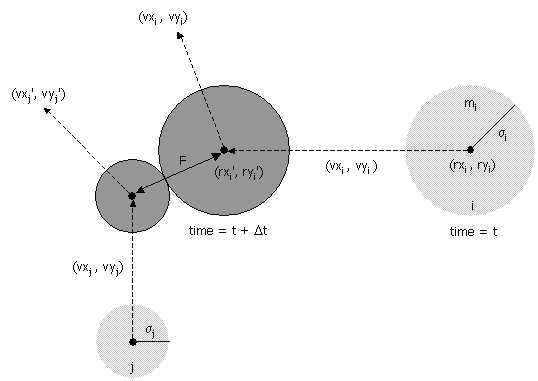
粒子 i 和 j 经过 \(\Delta t\) 时间发生碰撞,记 \(\sigma\) = \(\sigma_{i}\) + \(\sigma_{j}\),则有:
\(\sigma^{2}\) = \((rx_{i}'-rx_{j}')^{2}\) + \((ry_{i}'-ry_{j}')^{2}\)
又因为:
\(rx_{i}'\) = \(rx_{i}\) + \(\Delta t vx_{i}\), \(ry_{i}'\) = \(ry_{i}\) + \(\Delta t vy_{i}\)
\(rx_{j}'\) = \(rx_{j}\) + \(\Delta t vx_{j}\), \(ry_{j}'\) = \(ry_{j}\) + \(\Delta t vy_{j}\)
带入解 \(\Delta t\) 的二元方程得:
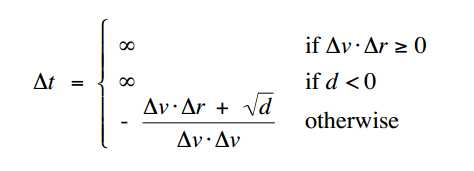
其中:
\(d = (\Delta v \cdot \Delta r)^{2} - (\Delta v \cdot \Delta v)(\Delta r \cdot \Delta r - \sigma^{2})\)
\(\Delta r = (\Delta rx, \Delta ry) = (rx_{j} - rx_{i}, ry_{i} - ry_{i})\)
\(\Delta v = (\Delta vx, \Delta vy) = (vx_{j} - vx_{i}, vy_{i} - vy_{i})\)
\(\Delta r \cdot \Delta r = (\Delta rx)^{2} + (\Delta ry)^{2}\)
\(\Delta v \cdot \Delta v = (\Delta vx)^{2} + (\Delta vy)^{2}\)
\(\Delta v \cdot \Delta r = (\Delta vx)(\Delta rx) + (\Delta vy)(\Delta ry)\)
然后,还有一件事,碰撞之后的速度问题,愣是没怎么懂。一般不是动量守恒加机械能守恒(碰撞前后总动能不变那个)联立算碰撞之后的速度,课程大概是把原始式子推来推去?最后用冲量来算也:
There are three equations governing the elastic collision between a pair of hard discs: (i) conservation of linear momentum, (ii) conservation of kinetic energy, and (iii) upon collision, the normal force acts perpendicular to the surface at the collision point. Physics-ly inclined students are encouraged to derive the equations from first principles; the rest of you may keep reading.
Between two particles. When two hard discs collide, the normal force acts along the line connecting their centers (assuming no friction or spin). The impulse (Jx, Jy) due to the normal force in the x and y directions of a perfectly elastic collision at the moment of contact is:
\(J_{x} = \frac{J\Delta rx}{\sigma}\),\(J_{y} = \frac{J\Delta ry}{\sigma}\) where \(J = \frac{2m_{i}m_{j}(\Delta v\cdot\Delta r)}{\sigma (m_{i} + m_{j})}\)
and where mi and mj are the masses of particles i and j, and σ, Δx, Δy and Δv ? Δr are defined as above. Once we know the impulse, we can apply Newton‘s second law (in momentum form) to compute the velocities immediately after the collision.
\(vx_{i}' = vx_{i} + J_{x}/m_{i}\), \(vx_{j}' = vx_{j} - J_{x}/m_{j}\)
\(vy_{i}' = vy_{i} + J_{y}/m_{i}\), \(vy_{i}' = vy_{i} - J_{y}/m_{j}\)
关于冲量怎么算的,这个链接(点我)好像有点靠谱,第一眼看上去挺像的,感觉不是重点,不管啦。另外,以上来自:booksite-61event。
现在,我们把上面讨论的预计碰撞时间和碰撞处理封装到 Particle 类里:
public class Particle {
private double rx, ry; // position
private double vx, vy; // velocity
private final double radius; // radius;
private final double mass; // mass
private int count; // number of collisions
public Particle(...) { }
public void move(double dt) { }
public void draw() { }
// predict collision with particle or wall
public double timeToHit(Particle that) { }
public double timeToHitVerticalWall() { }
public double timeToHitHorizontalWall() { }
// resolve collision with particle or wall
public void bounceOff(particle that) { }
public void bounceOffVeerticalWall() { }
public void bounceOffHorizontalWall() { }
}贴下例子,完整的参见:Particle.java。
public double timeToHit(Particle that) {
if (this == that) return INFINITY;
double dx = that.rx - this.rx, dy = that.ry - this.ry;
double dvx = that.vx - this.vx, dvy = that.vy - this.vy;
double dvdr = dx*dvx + dy*dvy;
if (dvdr > 0) return INFINITY;
double dvdv = dvx*dvx + dvy*dvy;
double drdr = dx*dx + dy*dy;
double sigma = this.radius + that.radius;
double d = (dvdr*dvdr) - dvdv * (drdr - sigma*sigma);
if (d < 0) return INFINITY;
return -(dvdr + Math.sqrt(d)) / dvdv;
}
public void bounceOff(Particle that) {
double dx = that.rx - this.rx, dy = that.ry - this.ry;
double dvx = that.vx - this.vx, dvy = that.vy - this.vy;
double dvdr = dx*dvx + dy*dvy;
double dist = this.radius + that.radius;
double J = 2 * this.mass * that.mass * dvdr / ((this.mass + that.mass) * dist);
double Jx = J * dx / dist;
double Jy = J * dy / dist;
this.vx += Jx / this.mass;
this.vy += Jy / this.mass;
that.vx -= Jx / that.mass;
that.vy -= Jy / that.mass;
this.count++;
that.count++;
}变量 count 记录粒子可能的碰撞次数,会被用于判断一个事件是否有效,像球 A 和球 B 本来会碰撞,但先和球 C 碰了的话,前者就无效了。具体怎么用,再来看看事件,我们把应该放入优先队列中的所有对象信息封装在一个私有类中(各种事件):
private class Event implements Comparable<Event> {
private double time; // time of event
private Particle a, b; // particles involved in event
private int countA, countB; // collision counts for a and b
public Event(double t, Particle a, Particle b) { }
public int compareTo(Event that) {
return this.time - that.time;
}
public boolean isValid() {
if (a != null && a.count() != countA) return false;
if (b != null && b.count() != countB) return false;
return true;
}
}如果事件从优先队列里取出来时变量 countA 和 countB 没有变化,说明 A B 粒子此前没有发生碰撞,事件仍是有效的;反之事件就是无效的,该丢弃取下一个。
有了上面这些铺垫,模拟的逻辑就很简单:从优先队列里取出最近的有效碰撞事件,按预计时间更新所有粒子的位置,更新参与碰撞的粒子的速度,预计参与碰撞粒子接下来可能发生的碰撞事件并插入优先队列,继续取有效碰撞,循环下去:
public class CollisionSystem {
private MinPQ<Event> pq; // the priority queue
private double t = 0.0; // simulation clock time
private Particle[] particles; // the array of particles
public CollisionSystem(Pariticle[] particles) { }
private void predict(Particle a) {
if (a == null) return;
for (int i = 0; i < particles.length; i++) {
double dt = a.timeToHit(particles[i]);
pq.insert(new Event(t + dt, a, particles[i]));
}
pq.insert(new Event(t + a.timeToHitVerticalWall(), a, null));
pq.insert(new Event(t + a.timeToHitHorizontalWall(), null, a));
}
public void simulate() {
pq = new MinPQ<Event>();
for (int i = 0; i < particle.lenght; i++)
predict(particles[i]);
pq.insert(new Event(0, null, null));
}
while (!pq.isEmpty()) {
Event event = pq.delMin();
if (!event.isValid()) continue;
Particle a = event.a;
Particle b = event.b;
for (int i = 0; i < particles.length; i++)
particles[i].move(event.time - t);
t = event.time;
if (a != null && b != null) a.bounceOff(b);
else if (a != null && b == null) a.bounceOffVerticalWall();
else if (a == null && b != null) b.bounceOffHorizontalWall();
else if (a == null && b == null) redraw();
predict(a);
predict(b);
}
}完整的参见:CollisionSystem.java。
最后,贴些效果图,也是很有趣啊,输入文件在 booksite-61event 上都有。
模拟花粉的布朗运动:java CollisionSystem < brownian2.txt
模拟扩散:java CollisionSystem < diffusion.txt

标签:变长数组 限制 模型 希尔排序 维护 完全二叉树 fir change 轨迹
原文地址:https://www.cnblogs.com/mingyueanyao/p/10215879.html