标签:accept ane 入口 作用 分享图片 style 代码 标记 each
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1011
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 23806 Accepted Submission(s): 6342
有n个洞穴编号为1~n,洞穴间有通道,形成了一个n-1条边的树, 洞穴的入口即根节点是1。
每个洞穴有x只虫子,并有价值y的金子,全部消灭完一个洞穴的虫子,就可以获得这个洞穴的y个金子.
现在要派m个战士去找金子,从入口进入。每次只有消灭完当前洞穴的所有虫子,才可以选择进入下一个洞穴。
一个战士可以消灭20只虫子,如果要杀死x只虫子,那么要x/20向上取整即(x+19)/20个战士。
如果要获得某个洞穴的金子,必须留下足够杀死所有虫子的战士数量, 即(x+19)/20个战士,然后这些留下战士就不能再去其它洞穴
其他战士可以继续走去其它洞穴,可以选择分组去不同的洞穴。
战士只能往洞穴深处走,不能走回头路
问最多能获得多少金子?
题意转自:https://blog.csdn.net/shuangde800/article/details/10069771
思路:典型的树形背包问题,这一题我用了两种方法写
特殊样例:
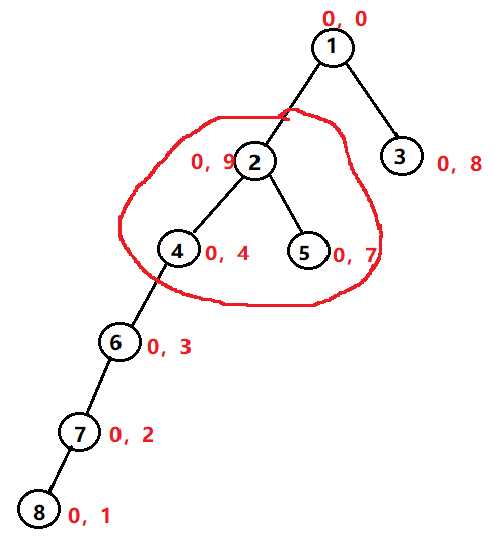
8 2 0 0 0 9 0 8 0 4 0 7 0 3 0 2 0 1 1 2 1 3 2 4 2 5 4 6 6 7 7 8
27
1.这种方法是我在一开始的代码一直wa然后看别人的思路改的,其中dp[i][j]表示以i节点构成的子树在有j个士兵的情况下最多可以获得的金钱数
代码:
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int val[110];//价值 int wet[110];//花费 bool vt[110];//标记数组 struct{//链式前向星 int v,next; }edge[220]; int cnt; int head[110]; void add(int u,int v){//加边 edge[cnt].v=v; edge[cnt].next=head[u]; head[u]=cnt++; } int dp[110][110];//dp[i][j]表示在以i个节点为根节点构成的子树中用j个士兵可以获得的最大金钱数 int n,m; void dfs(int k){ vt[k]=true; bool lg=true; if(wet[k]==0){//如果k是叶子节点并且它的花费为0,那么它的花费就要加一(因为你至少要派一个士兵去到这个房间才能获得该房间的金钱) for(int i=head[k];i!=-1;i=edge[i].next){ if(!vt[edge[i].v]) lg=false; } if(lg) wet[k]++; } for(int i=0;i<wet[k];i++)//初始化,要到达当前房间,需要的士兵数至少是wet[k],当士兵数小于wet[k]时可以获得的金钱数就为0 dp[k][i]=0; for(int i=wet[k];i<=m;i++){//当士兵数不少于当前房间的花费时,它可以获得当前房间的金钱 dp[k][i]=val[k]; } for(int i=head[k];i!=-1;i=edge[i].next){//看看是否可以往它下面的房间走使得得到的金钱数更多 if(!vt[edge[i].v]){ dfs(edge[i].v);//递归子节点 for(int j=m;j>=wet[k];j--){//尝试用子节点更新父节点 for(int l=wet[k];l<j;l++){ dp[k][j]=max(dp[k][j],dp[k][l]+dp[edge[i].v][j-l]);/*其中dp[k][]中保留着用上一个子节点更新父节点后的值, 相当于多重背包的上一样物品更新完后的背包,而当前子节点的值(dp[edge[i].v][])相当于当前物品*/ } } } } } int main(){ while(scanf("%d%d",&n,&m)!=EOF&&(n!=-1||m!=-1)){ fill(head,head+101,-1);//初始化 fill(vt,vt+101,false); for(int i=1;i<=n;i++){ scanf("%d%d",&wet[i],&val[i]); wet[i]=wet[i]/20+(wet[i]%20!=0);//转换一下花费,如果不足20个虫子也要派一个士兵 } int u,v; cnt=0; for(int i=1;i<n;i++){//边是双向的 scanf("%d%d",&u,&v); add(u,v); add(v,u); } dfs(1); if(m==0)//特判一下,当你没有士兵时无论如何都得不到金钱 printf("0\n"); else printf("%d\n",dp[1][m]); } return 0; }
2.这种方法是我最开始想到的,但是不知道为什么一直wa,然后找了半天才发现是自己没有充分理解 “如果当前节点花费为0且为叶子节点,那么它的花费要加一”这句话,我只考虑了完整的树的叶子节点花费为0的情况,而没有考虑到当我选出这棵树的部分的时候它叶子节点花费为0的情况.
在这种方法中,我的dp[i][j]表示的是以第i个节点为根节点时,向它的所有子树(不包括根节点)派遣j个士兵最多可以获得的金钱树
代码
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int val[110]; int wet[110]; bool vt[110]; struct{//链式前向星 int v,next; }edge[220]; int cnt; int head[110]; void add(int u,int v){ edge[cnt].v=v; edge[cnt].next=head[u]; head[u]=cnt++; } int dp[110][110];//dp[i][j]表示向以i为根节点(不包括i)的所有子树中派遣j名士兵最多可以获得的金钱数 int n,m; void dfs(int k){ for(int i=0;i<=m;i++){//初始化全部为0 dp[k][i]=0; } vt[k]=true; for(int i=head[k];i!=-1;i=edge[i].next){ if(!vt[edge[i].v]){ dfs(edge[i].v); for(int j=m;j>=wet[edge[i].v]&&j>=1;j--){ for(int l=0;l<=j-wet[edge[i].v];l++){ //printf("QQQ%d %d",dp[k][j-l-wet[edge[i].v]-(l==0&&wet[edge[i].v]==0)],dp[edge[i].v][l]); dp[k][j]=max(dp[k][j],dp[k][j-l-wet[edge[i].v]-(l==0&&wet[edge[i].v]==0)]+dp[edge[i].v][l]+val[edge[i].v]); //你当前选择用子节点更新它的父节点时,就算当前子节点的花费为0你也至少要派一个士兵 //(l==0&&wet[edge[i].v]==0)的作用就是判断是否有叶节点的wet为0 ,l==0代表现在是用叶节点来更新 //printf("QQQ%d %d %d %d %d %d \n",k,edge[i].v,j,l,j-l-wet[edge[i].v]-(l==0&&wet[edge[i].v]==0),dp[k][j]); } //printf("qqqq%d %d %d\n",k,j,dp[k][j]); } } } } int main(){ while(scanf("%d%d",&n,&m)!=EOF&&(n!=-1||m!=-1)){ fill(head,head+101,-1);//初始化 fill(vt,vt+101,false); for(int i=1;i<=n;i++){ scanf("%d%d",&wet[i],&val[i]); wet[i]=wet[i]/20+(wet[i]%20!=0);//简化花费 } int u,v; cnt=0; for(int i=1;i<n;i++){//边是双向的 scanf("%d%d",&u,&v); add(u,v); add(v,u); } dfs(1); if(m==0)//特判 printf("0\n"); else{ if(m>=wet[1])//如果当前的士兵数大于根节点的花费数 dp[1][m-wet[1]]+=val[1]; printf("%d\n",dp[1][m-wet[1]]);//如果小于的话不要else也是输出0 } } return 0; } /*
8 2 0 0 0 9 0 8 0 4 0 7 0 3 0 2 0 1 1 2 1 3 2 4 2 5 4 6 6 7 7 8
27
*/
当前我已经用节点5更新完了节点2,现在我用节点4来更新节点2,当更新dp[2][1]时,由于我dp的特殊性,当用dp[4][0]来更新dp[2][1]时,如果不注意上面的情况,就会发生
dp[2][1]=max(dp[2][1],dp[2][1]+dp[4][0]+val[4]),为什么呢,因为当前4节点的花费为零,如果我想只加上4节点时(即用dp[4][0]来更新时),会出现由于4节点花费为0而可以不用派士兵就可以得到它节点上的金钱的情况,而这种情况是不合法的,因为你至少要派一名士兵去4节点拿钱,而它不能走回头路,只能往下走。
标签:accept ane 入口 作用 分享图片 style 代码 标记 each
原文地址:https://www.cnblogs.com/cglongge/p/10305771.html