标签:就是 col root int nbsp print its long bre
题目:
给出一棵树的BFS和DFS序列,输出这棵树中每个结点的子结点列表。BFS和DFS序列在生成的时候,当一个结点被扩展时,其所有子结点应该按照编号从小
到大的顺序访问。
思路:
一开始是想根据BFS和DFS序列来建树做这个题,但是利用BFS处理好分层之后就卡死了。
1.可以先处理好BFS中每个结点的距离。
2.在输入DFS时判断如果x点到根的距离比栈顶元素到根的距离多于1,那x就是栈顶元素的孩子结点,将x压入栈中。如果距离等于1说明x与栈顶元素是兄弟结点,
弹出栈定元素。
总结:
1.在DFS序列中距离相差为1的结点而且在BFS中距离也为1的两个结点的情况:父子关系,父亲结点是BFS所在层最右边的结点。
2.在DFS序列中距离相差为1的结点但在BFS中距离大于1:必定是父子关系。
3.在DFS序列中距离相差为1的结点但在BFS中距离小于1:说明在DFS序列中靠后的结点在BFS中的层数要小于DFS序列中靠前的结点。
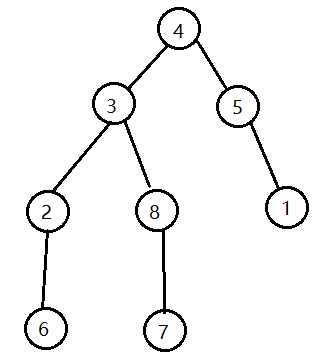
如下边这个例子:
BFS:4 3 5 1 2 8 6 7
DFS:4 3 2 6 8 7 5 1
代码:
#include <bits/stdc++.h> #define inf 0x3f3f3f3f #define MAX 1000000009 #define FRE() freopen("in.txt","r",stdin) #define FRO() freopen("out.txt","w",stdout) using namespace std; typedef long long ll; const int maxn = 1010; int bfs[maxn],n; int main() { //FRE(); int root,x; while(scanf("%d",&n)!=EOF) { for(int i = 0; i<n; i++) { scanf("%d",&x); bfs[x] = i; } stack<int> sta; vector<int> ans[maxn]; scanf("%d",&root); sta.push(root); for(int i=1; i<n; i++) { scanf("%d",&x); while(true) { if((sta.top()==root) || (bfs[x]-bfs[sta.top()]>1) ||//对应总结中的1、2点 (bfs[x]-bfs[sta.top()]==1&&x<sta.top())) { ans[sta.top()].push_back(x); sta.push(x); break; } else { sta.pop(); } } } for(int i=1; i<=n; i++) { printf("%d:",i); for(int j=0; j<ans[i].size(); j++) { printf(" %d",ans[i][j]); } printf("\n"); } } return 0; }
UVA - 10410 Tree Reconstruction(栈处理递归)
标签:就是 col root int nbsp print its long bre
原文地址:https://www.cnblogs.com/sykline/p/10305931.html