两道题学习动态规划

标签：学习   www.   else   需要   img   png   越界   数据   不容易   

动态规划，是为了解决overlap sub-problem（重叠子问题）。最重要的是状态的定义和状态转移方程的定义，而把状态转移方程确定，一般是最难的一步。
学习动态规划，可以先把递归过程理解清楚，再使用非递归的方法，来求解问题，来避免重复计算。

参考：
正月点灯笼-动态规划
下面是两道例题：

• 在一个数组arr中，找出一组不相邻的数字，使得最后的和最大。

input
arr=1 2 4 1 7 8 3

output
15

opt[i]表示下标为i的最佳方案， + - 表示选与不选该数，例如opt[6]，选了下标为6的数，那么opt[6] = opt[4] + arr[6]，如果不选，那么opt[6] = opt[5];接下来就是求两个的最大值，得到最佳。下面的图显示了他们的递推关系，也出现了重叠子问题。

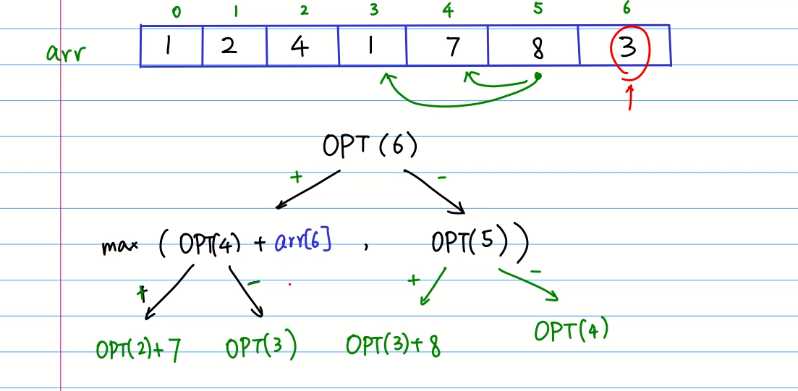
接着就可以找到递推方程，也就是状态转移方程

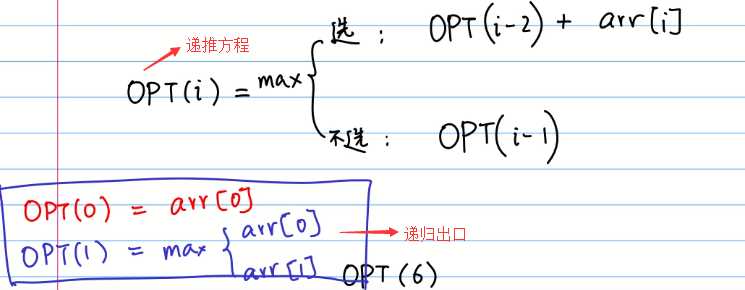
一旦我们确定出这个方程，就可以很快的用递归来实现

int rec_opt(int a[],int i)
{
    if( i == 0 )
    {
        return a[0];
    }else if(i == 1)
    {
        return max(a[0],a[1]);
    }else
    {
        int t1 = rec_opt(a,i-2) + a[i];
        int t2 = rec_opt(a,i-1);
        return max(t1,t2);
    }
}

接下来就是解决重叠子问题，使用非递归来实现

int dp_opt(int a[])
{
    opt[0] = a[0];
    opt[1] = max(a[0],a[1]);
    for(int i = 2; i < N; i++)
    {
        int t1 = opt[i-2]+a[i];
        int t2 = opt[i-1];
        opt[i] = max(t1,t2);
    }
    return 0;//这里我直接返回了0，实际上最后的最佳方案就是opt[6],因为测试数据包含7个数据。
}

• 给定一个正整数s, 判断一个数组arr中，是否有一组数字加起来等于s。

input
arr=3 34 4 12 5 3
s=9
s=13

output
True
False

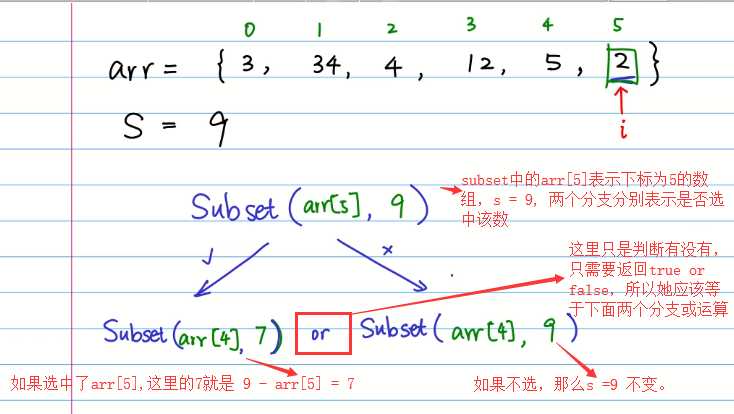
接下里就是比较难找的递归出口情况
前两种情况很快就能得出，第三种情况不容易想到

有了上图的状态方程，就可以写出递归了

bool rec_subset(int a[], int i, int s)
{
    if(s == 0)//递归的三个出口
        return true;
    else if (i == 0)
        return a[0] == s;
    else if(a[i] > s)
        return rec_subset(a,i-1,s);
    else{
        int t1 = rec_subset(a,i-1,s - a[i]); //选
        int t2 = rec_subset(a,i-1,s);//不选
        if(t1 || t2)
            return true;
    }
}

接下来就是比较麻烦的非递归实现
这里设置一个二维数组来实现

下面是代码实现

bool dp_subset(int a[],int n,int s)
{
    int **subset;
    int i,j;

    subset = (int **)malloc(sizeof(int *)*n);
    for (i=0; i < n; i++)
        subset[i] = (int *)malloc(sizeof(int)*(s+1));
    
    for(i = 0; i <= s; i++)
    {
        subset[0][i] = 0; //将第0行设置为false
    }
    for(i = 0; i < n; i++)
        subset[i][0] = 1;//将第0列设置为false

    if(a[0] <= s)
    {
        subset[0][a[0]] = 1;//s == arr[0]，subset[0][a[0] = 1;这里需要判断，否则可能会发生越界
    }

    for(i = 1; i < n; i++)
    {
        for(j = 1; j <= s; j++)
        {
            if(a[i] > j)
                subset[i][j] = subset[i-1][j]; //递归第三个出口判断
            else
            {
                //接下来就是递推式中的两种情况 or
                int t1 = subset[i-1][j-a[i]];
                int t2 = subset[i-1][j];
                subset[i][j] = t1 || t2;
            }
        }

    }

    int temp = subset[n-1][s];
    for(i = 0; i < n;i++)
        free(subset[i]);
    free(subset);

    return temp;
}

所以，动态规划 = 用数组记录中间过程的递归？

两道题学习动态规划

标签：学习   www.   else   需要   img   png   越界   数据   不容易   

原文地址：https://www.cnblogs.com/hish/p/10305980.html