标签:理解 span 比较 idt 一个 ips 证明 com 通过
splay啊,是一种优(la)美(ji)的数据结构
它的操作主要就是Splay伸展操作
但是在讲splay操作之前,我们得讲一下旋转
如果学过treap可以考虑跳过
你先不用管为什么要旋转,如果你有耐心看完就会知道了
首先,splay是一棵二叉查找树(Binary Search Tree简称BST),它的节点必须满足:
左儿子小于它,右儿子大于它
(以上讨论的是权值)(Tips:不一定严格按照这样的规则,有时候从方便角度会写成小于等于等)
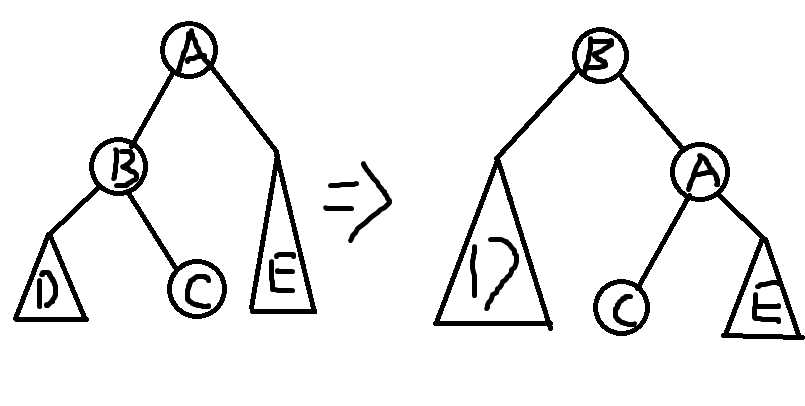
那么我们的旋转是什么呢?要把儿子旋转到父亲的位置且不破坏BST的结构。
那我们先考虑左儿子转上去吧:
左儿子的值比父亲小,那么这说明转上去以后,父亲是左儿子的右儿子(画图理解一下吧)
那么左儿子的右儿子怎么办呢?可以得出左儿子<右儿子<父亲,那么左儿子的右儿子应该变成父亲的左儿子
(上演真实伦理大戏)
同理,右儿子也是类似的,你可以把上面的图箭头反过来
首先,为什么要进行伸展操作呢?
因为BST在更新和修改中会变得非常丑陋,如:
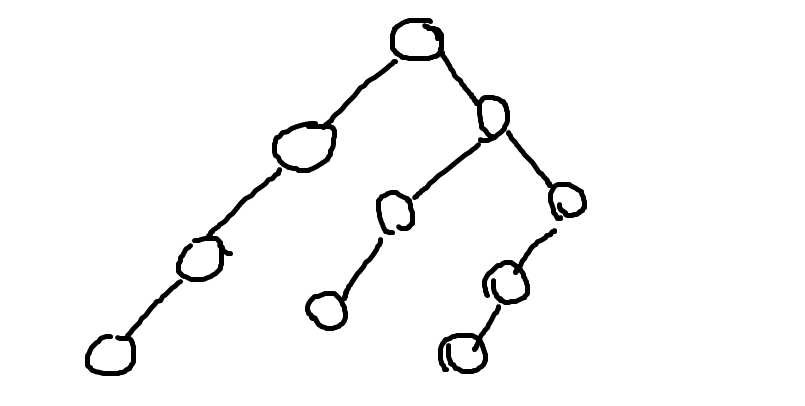
也就是说,树有可能会退化成链或者树的结构不优美
为了应对这个,我们需要有意识的对树进行旋转
在treap中我们用堆的性质来决定是否旋转,而在splay中,我们用的就是伸展操作
在伸展操作中,我们要做的是将当前节点旋转至成为目标节点的儿子(特殊的,当目标节点为0时,结束旋转后,当前节点是根)
一次伸展操作(我觉得叫冲程)分为两次旋转(注意操作是一次,过程才是全部)
对于这两次旋转,我们需要分类讨论:
1、正常旋转两次x(将x提到其祖父的位置)
2、当父亲和儿子在同一边时,先旋转父亲,再旋转儿子
这个同一边是什么操作?
假设父亲是祖父的右儿子,儿子也是父亲的右儿子,那么它们在同一边
为什么呢?请看图
我们发现如果正常旋转则会形成链,那么按照讨论的方法旋转呢?
那就XXXX了
3、当祖父已经是目标节点时,只旋转一次,然后结束
这个不用解释吧
通过伸展操作,我们可以进行非常多很捞的操作,因为伸展前后其都满足BST性质,可以通过这个圈出要修改的区间啥的
非常简单,将要求的点旋至根后往左节点走一步,一直往右到不能走为止即可(显然)
--上面讲的是前驱
splay的区间操作都是基于这样一个基础上的:
将排名l-1的节点伸展至根节点,排名r+1的节点伸展至根节点的右儿子处
这样r+1节点的左儿子就是l~r的区间了
首先逐层翻转是正确的,有兴趣可以自查证明
和线段树非常相似,具体就是要打上懒惰标记(不过由于翻转是可以相互抵消的,所以可以位运算a^1或者!a)
然后重点就是要在每次改变树的结构的操作之前下传标记
有两种做法,不过操作1比较捞
1、一个一个插入啊
2、将这几个数据再建一棵小的splay,然后将需要操作的区间旋至根,需要操作的区间的前驱旋至根的右儿子
最后把要插入的数据建的树的树根接到前驱的左儿子处即可
(这是在某个元素后插入数据的操作)
标签:理解 span 比较 idt 一个 ips 证明 com 通过
原文地址:https://www.cnblogs.com/mastervan/p/10307009.html