标签:.com 分享 sub com 优化 margin 运行 bsp 相关
罚函数法的基本思想是借助罚函数把约束问题转化为无约束问题,然后用无约束最优方法来求解。
构造罚函数:在可行点,辅助函数的值等于原来的目标函数值;在不可行点,辅助函数值等于原来的目标函数值加上一个很大的正数。可写成形如下式:
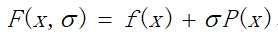
目标函数:
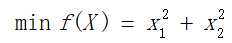
约束条件:

其相关代码如下:
clc
syms x1 x2 e; % e为罚因子
m(1)=1;c=10;a(1)=0;b(1)=0; % c为递增系数 赋初值
f=x1^2+x2^2+e*(1-x1)^2; % 构造罚函数
f0(1)=0;
%求偏导、海森阵
fx1=diff(f,‘x1‘);
fx2=diff(f,‘x2‘);
fx1x1=diff(fx1,‘x1‘);
fx1x2=diff(fx1,‘x2‘);
fx2x1=diff(fx2,‘x1‘);
fx2x2=diff(fx2,‘x2‘);
for k=1:100 %外点法e迭代循环
x1=a(k);x2=b(k);e=m(k);
for n=1:100 %牛顿法求最优值
f1=subs(fx1); %求梯度值和海森矩阵
f2=subs(fx2);
f11=subs(fx1x1);
f12=subs(fx1x2);
f21=subs(fx2x1);
f22=subs(fx2x2);
if(double(sqrt(f1^2+f2^2))<=0.000001) %最优值收敛条件
a(k+1)=double(x1);b(k+1)=double(x2);f0(k+1)=double(subs(f));
break;
else
X=[x1 x2]‘-inv([f11 f12;f21 f22])*[f1 f2]‘;
x1=X(1,1);x2=X(2,1);
end
end
if(double(sqrt((a(k+1)-a(k))^2+(b(k+1)-b(k))^2))<=0.000001)&&(double(abs((f0(k+1)-f0(k))/f0(k)))<=0.000001) %迭代收敛条件
disp(‘最优坐标 x1:‘),disp(a(k+1))%输出最优点坐标,迭代次数,最优值
disp(‘最优坐标 x2:‘),disp(b(k+1))
disp(‘迭代次数‘),disp(k)
disp(‘最优值‘),disp(f0(k+1))
break;
else
m(k+1)=c*m(k);
end
end
运行结果如下:
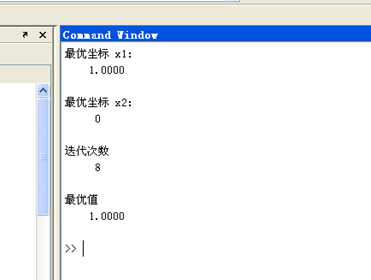
标签:.com 分享 sub com 优化 margin 运行 bsp 相关
原文地址:https://www.cnblogs.com/zhuhongzhous/p/10308855.html