麻省理工公开课：线性代数 第8课 求解Ax=b：可解性和解的结构

标签：http   spl   网易公开课   splay   dai   描述   两种   分享图片   open   

参考资料：

网易公开课：http://open.163.com/special/opencourse/daishu.html　　麻省理工公开课：线性代数

教材：Introduction to Linear Algebra, 4th edition  by Gilbert Strang

链接：https://pan.baidu.com/s/1bvC85jbtOVdVdw8gYMpPZg
提取码：s9bl

假设：$A$为$3\times 4$长方形矩阵（线性相关），求解$A\mathbf{x}=\mathbf{b}$

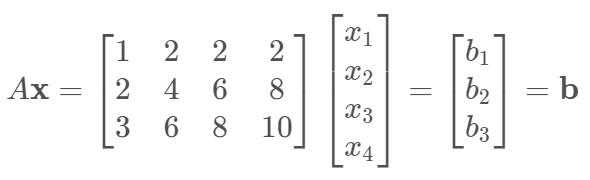
一、增广矩阵消元 augmented matrix

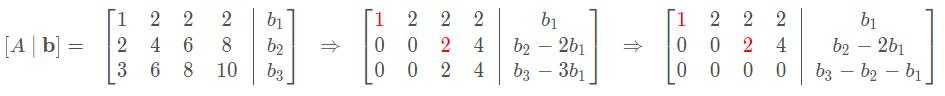
（1）$A\mathbf{x}=\mathbf{b}$有解条件　　//两种等价描述方式

• 当且仅当$\mathbf{b}$位于矩阵$A$的列空间$C(A)$内
• 如果矩阵$A$的行线性组合在消元过程中得到全零行，$\mathbf{b}$的相同组合也必须为0，本例中$b_3-b_2-b_1$必须为零

二、求解$A\mathbf{x}=\mathbf{b}$的所有解

（1）求解$A\mathbf{x}=\mathbf{b}$的特解$\mathbf{x}_{particular}$：令所有的自由变量为零，求解所有主变量的值

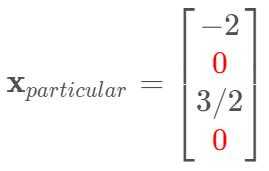
（2）求解$A\mathbf{x}=\mathbf{0}$对应的零空间解$\mathbf{x}_{nullsapce}$

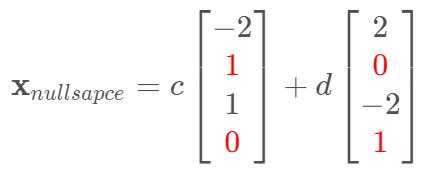
（3）$A\mathbf{x}=\mathbf{b}$的完整解为：$\mathbf{x}_{complete}=\mathbf{x}_{particular}+\mathbf{x}_{nullsapce}$，本例为经过$\mathbf{x}_{particular}$的某二维平面（不包含原点，不是子空间）

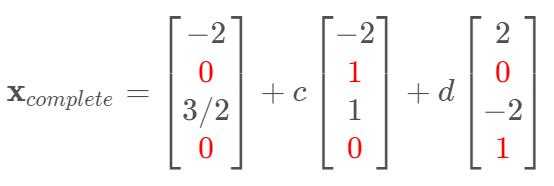
注：$A\mathbf{x}_p=\mathbf{b}，A\mathbf{x}_n=\mathbf{0} \Rightarrow A(\mathbf{x}_p+\mathbf{x}_n)=\mathbf{b}$

三、假设矩阵$A$为$m\times n$矩阵，秩为$r$

（1）秩的定义：主元的个数　　//$r\leq m, r\leq n$

（2）列满秩：$r=n<m$　　//各列线性无关

• 主元个数为$n$，无自由变量，零空间$N(A)$仅包含零向量
• 若$A\mathbf{x}=\mathbf{b}$有解，则仅有唯一解$\mathbf{x}_{particular}$　　//$\mathbf{x}_{particular}$要么无解，要么有唯一解

　　注：$A\mathbf{x}=\mathbf{b}$有0或1个解

（3）行满秩：$r=m<n$　　//各行线性无关

• 主元个数为$m$，自由变量个数为$n-m$
• 对于任意$\mathbf{b}$，$A\mathbf{x}=\mathbf{b}$都有解　　//因为每行均存在主元，则消元过程中对$\mathbf{b}$无任何限制，一定有解

　　注：$A\mathbf{x}=\mathbf{b}$有无穷个解

（4）满秩方阵：$r=m=n$

• 矩阵可逆，零空间只有零向量
• 行最简矩阵$R=I$
• $A\mathbf{x}=\mathbf{b}$一定有唯一解$\mathbf{x}=A^{-1}\mathbf{b}$

　　注：$A\mathbf{x}=\mathbf{b}$有唯一解

（5）非满秩矩阵：$r<m, r<n$

　　注：$A\mathbf{x}=\mathbf{b}$有0或无穷个解

注：矩阵的秩决定了方程组解的个数

麻省理工公开课：线性代数 第8课 求解Ax=b：可解性和解的结构

标签：http   spl   网易公开课   splay   dai   描述   两种   分享图片   open   

原文地址：https://www.cnblogs.com/hg-love-dfc/p/10309526.html