标签：假设 flag == pac 初始 onclick bsp 缺陷 方法
队列的定义： 只允许在一端进行操作，在另一端进行删除操作的线性表。
队列是一种先进先出的线性表，简称FIFO，允许插入的一端称为队尾，允许删除的一端称为队头。
原因：
假设一个队列有n个元素，则顺序存储的队列需要建立一个大于n的数组，并把队列的所有元素存储在数组的前n个单元，数组下标为0的一端即为对头。
所谓的入队，就是在队尾追加一个元素，不需要移动任何元素，所以时间复杂度为O(1).
队列的出队是在对头，即下标为0的位置，也就意味着，队列中的所有位置都得向前移动，以保证下标为0的位置，即对头不为空。此时时间复杂度为O(n)。
可是有时候想想，为什么出队列时一定要全部移动呢？如果不限制队列的元素一定要存储在数组的前n个单元，出队的性能就会大大增加。也就是说，队头不需要一定在下标为0的位置。
但如果不全部移动的话，又会引入新的问题？那就是数组的 “假溢出”
为了避免当只有一个元素时，对头和队尾重合使得处理变得麻烦，所以引入两个指针，front指针指向对头元素，rear指针指向队尾元素的下一个元素。这样当front等于rear时，不是队列中有一个元素，而是表示空队列。
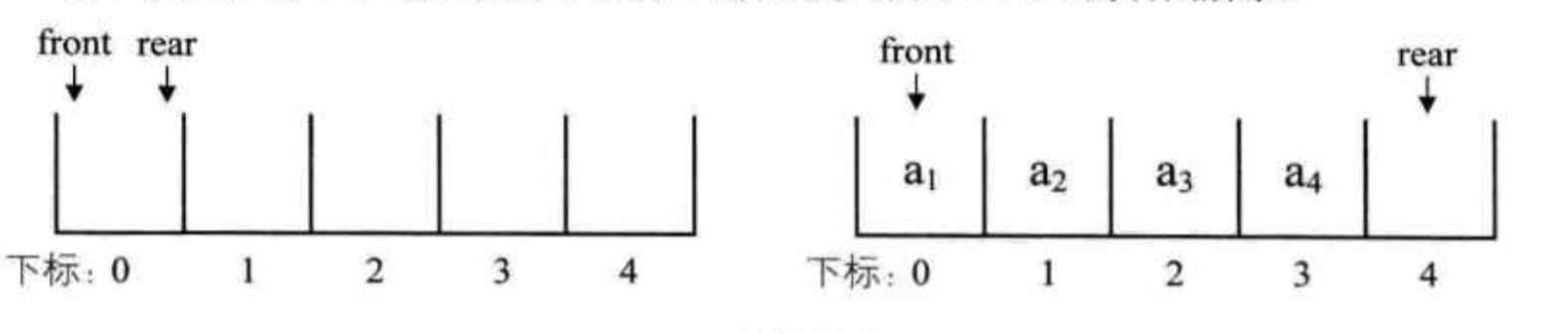
假设数组的长度为5，空队列及初始状态如左图所示，front与rear指针都指向下标为0的位置。当队列中有4个元素时，front指针不变，rear指针指向下标为4的位置。
此时出队两个元素，则front指针指向下标为2的位置，rear不变。再入队一个元素，front指针不变，此时rear指针移动到数组之外，这就产生了 “假溢出” 现象。
为了解决这种假溢出的现象。我们引入了循环队列
我们把队列的头尾相接的顺序存储结构称之为循环队列。
为了解决假溢出的现象，就是当队列满了，我们再从头开始存数据，这是时候头尾已经相连了，就形成了循环队列。
继续刚才的例子，将rear指针指向下标为0的位置，就不会导致rear指针指向不明的问题。
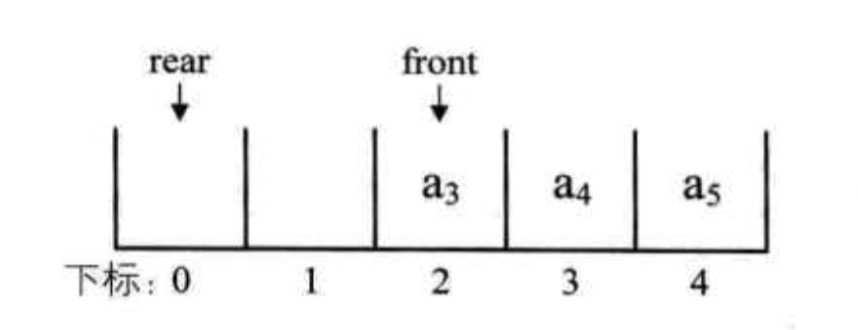
接着入队两个元素，会发现rear指针与front重合了
此时问题又来了，刚才说了，当rear等于front时，表示是空队列，现在当队列满时，rear也等于front。那么如何判断队列到底是空的还是满的了？
我们有两个判断方法：
办法一是设置标志变量flag，当front = rear ,且flag =0 为队列空，当front =rear ，且flag =1 时队列满。
办法二是当队列为空时，条件是front = rear ,当队列满时，我们修改其条件，保留一个元素的空间，也是就是说，当队列满时，数组里面还有一个空闲的单元。
例如下图就表示了队列已经满了
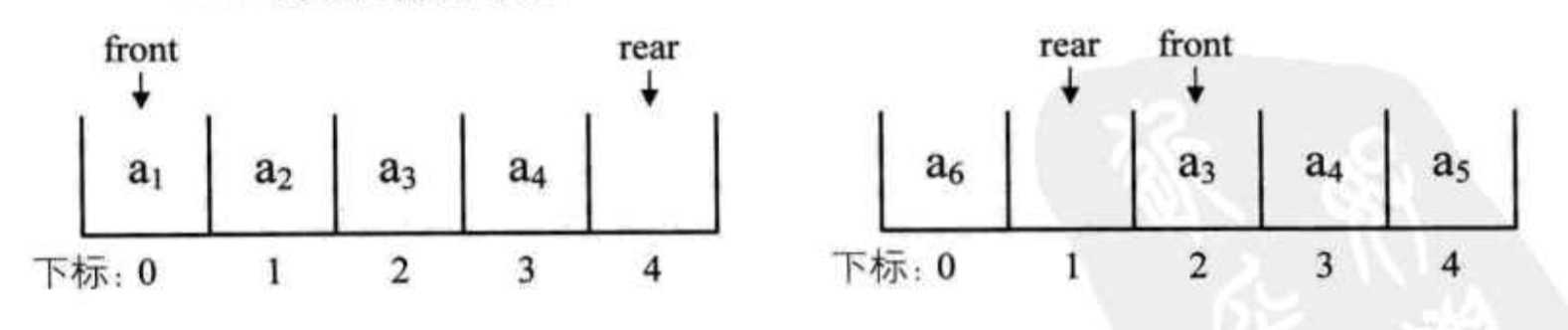
就不能再插入元素了。
由于队列是循环队列，rear可能比front大，也可能比front小，所以假设队列的最大尺寸为QueueSize, 队列满的判断条件改为（rear + 1）%QueueSize = front. 队列的长度为（rear - front + QueueSize）% QueueSize.
以上的部分文字和图片Copy大佬：https://www.cnblogs.com/muzijie/p/5650187.html
typedef struct{
int data[MAXSIZE]; //容量
int front; //前驱下标
int real; //后继下标
}SqQueue;
1 /*初始化队列*/
2 void InitQueue(SqQueue* Q){
3 Q->front=0;
4 Q->real=0; //前驱和后继都指向0
5 }
1 /*求一个循环队列的长度*/
2 int QueueLength(SqQueue Q){
3
4 return (Q.real-Q.front+MAXSIZE)%MAXSIZE;
5 }
1 /*入队操作*/
2 int EnQueue(SqQueue* Q,int e){
3 if(FullQueue(*Q))
4 return 0;
5 Q->data[Q->rear]=e;
6 Q->rear = (Q->rear+1)%MAXSIZE; //将rear指针向后移一位
7 /*若到最后则转到数组头部*/
8 }
1 /*出队操作*/
2 int DeQueue(SqQueue* Q){
3 int e;
4 if(Q->front ==Q->rear){
5 return 0;
6 }
7 e = Q->data[Q->front];
8 Q->front = (Q->front+1)%MAXSIZE;
9 return e;
10 }
其它操作的实现代码
1 #include <stdio.h>
2 #define MAXSIZE 20
3
4 typedef struct{
5
6 int data[MAXSIZE]; //容量
7 int front; //前驱下标
8 int rear; //后继下标
9
10 }SqQueue;
11
12 /*初始化队列*/
13 void InitQueue(SqQueue* Q){
14 Q->front=0;
15 Q->rear=0; //前驱和后继都指向0
16 }
17
18 /*求一个循环队列的长度*/
19 int QueueLength(SqQueue Q){
20
21 return (Q.rear-Q.front+MAXSIZE)%MAXSIZE;
22 }
23
24 /*判断是否队满*/
25 int FullQueue(SqQueue Q){
26 if(QueueLength(Q) ==MAXSIZE)
27 return 1;
28 else
29 return 0;
30 }
31
32 /*入队操作*/
33 int EnQueue(SqQueue* Q,int e){
34 if(FullQueue(*Q))
35 return 0;
36 Q->data[Q->rear]=e;
37 Q->rear = (Q->rear+1)%MAXSIZE; //将rear指针向后移一位
38 /*若到最后则转到数组头部*/
39 }
40
41 /*出队操作*/
42 int DeQueue(SqQueue* Q){
43 int e;
44 if(Q->front ==Q->rear){
45 return 0;
46 }
47 e = Q->data[Q->front];
48 Q->front = (Q->front+1)%MAXSIZE;
49 return e;
50 }
51
52 int main(){
53
54 SqQueue s;
55 InitQueue(&s);
56 for(int i=0;i<10;i++){
57 EnQueue(&s,i);
58 }
59
60 for( i=0;i<10;i++){
61 printf("出队元素：%d\n",DeQueue(&s));
62 }
63
64 return 0;
65 }
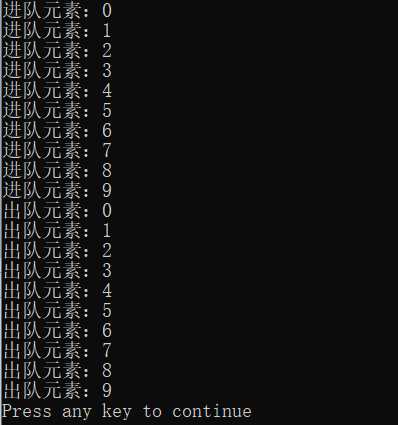
附上Java代码实现
1 package queue; 2 3 public class Test { 4 5 public static void main(String[] args) { 6 7 Queue queue = new Queue(); 8 System.out.println("初始化队..."); 9 queue.InitQueue(queue); 10 System.out.println("入队操作..."); 11 for (int i = 0; i < 10; i++) 12 System.out.print(queue.EnQueue(queue, i) + " "); 13 14 System.out.println(""); 15 System.out.println("判断对是否为空..." + queue.ElmptyQueue(queue)); 16 17 System.out.println("出队操作..."); 18 for (int j = 0; j < 10; j++) 19 System.out.print(queue.DeQueue(queue) + " "); 20 21 System.out.println(""); 22 System.out.println("判断对是否为空..." + queue.ElmptyQueue(queue)); 23 } 24 25 }
1 package queue; 2 3 public class Queue { 4 5 int data[] = new int[20]; 6 int rear; // 后下标 7 int front; // 前下标 8 9 /** 10 * 初始化队列 11 */ 12 public void InitQueue(Queue Q) { 13 Q.front = 0; 14 Q.rear = 0; 15 } 16 17 /** 18 * 入队操作 19 */ 20 public int EnQueue(Queue Q, int e) { 21 if (FullQueue(Q) == 1) 22 return 0; 23 24 Q.data[Q.rear] = e; 25 Q.rear = (Q.rear + 1) % 20; 26 27 return e; 28 } 29 30 /** 31 * 出队操作 32 */ 33 public int DeQueue(Queue Q) { 34 int e; 35 if (QueueLength(Q) == 0) 36 return 0; 37 38 e = Q.data[Q.front]; 39 Q.front = (Q.front + 1) % 20; 40 return e; 41 } 42 43 /** 44 * 判断是否队满 45 */ 46 public int FullQueue(Queue Q) { 47 if ((Q.rear + 1) % 20 == Q.front) // 判断是否为队满 48 return 1; 49 else 50 return 0; 51 } 52 53 /** 54 * 返回队长度 55 */ 56 public int QueueLength(Queue Q) { 57 58 return (Q.rear - Q.front + 20) % 20; 59 } 60 61 /** 62 * 判断是否队空 63 */ 64 public boolean ElmptyQueue(Queue Q) { 65 if (Q.front == Q.rear) 66 return true; 67 return false; 68 } 69 }
完毕 - -
标签：假设 flag == pac 初始 onclick bsp 缺陷 方法
原文地址：https://www.cnblogs.com/liuzeyu12a/p/10309361.html
