标签：mat 图片 src row red inf line time style
参考资料：
网易公开课：http://open.163.com/special/opencourse/daishu.html 麻省理工公开课：线性代数
教材：Introduction to Linear Algebra, 4th edition by Gilbert Strang
链接：https://pan.baidu.com/s/1bvC85jbtOVdVdw8gYMpPZg
提取码：s9bl
假设：$m\times n$矩阵$A$
一、矩阵$A$的列空间：$C(A)$
（1）是$R^m$的子空间
（2）维数：矩阵$A$的秩$r$ //$A\mathbf{x}=0$主元变量的数目
（3）基：$r$个主列
二、矩阵$A$的零空间：$N(A)$
（1）是$R^n$的子空间
（2）维数：$A\mathbf{x}=0$自由变量的数目$n-r$
（3）基：自由变量对应的$n-r$个特解
三、矩阵$A$的行空间：$C(\color{red}{A^T})$ //矩阵$A$所有行的线性组合；或者矩阵$A$的转置$A^T$所有列的线性组合
（1）是$R^n$的子空间
（2）维数：矩阵$A^T$的秩$r$ //$rank(A)=rank(A^T)$
（3）基：行最简矩阵$R$的前$r$行 //不一定是$A$的前$r$行
注：矩阵$A$和行最简矩阵$R$的行空间相同（$C(A^T)=C(R^T)$），列空间不同（$C(A)\neq C(R)$） //“行变换”不影响行空间(基一致)，但是会改变列空间
四、矩阵$A$的转置的零空间：$N(\color{red}{A^T})$ //左零空间：$A^T\mathbf{y}=\mathbf{0} \Rightarrow \color{red}{\mathbf{y}^TA=\mathbf{0}^T}$
（1）是$R^m$的子空间
（2）维数：$m-r$
（3）基：变换矩阵$E$的最下方$m-r$行
利用高斯-约旦消元法（第3课）求解变换矩阵$E$使得$EA=R$ //当m=n，且$A$可逆时，$R=I, E=A^{-1}$
变换矩阵$E$的最下方$m-r$行正是使得$A$各行线性组合为0的系数（左乘相当于行组合），即为矩阵$A^T$零空间的基
示例：
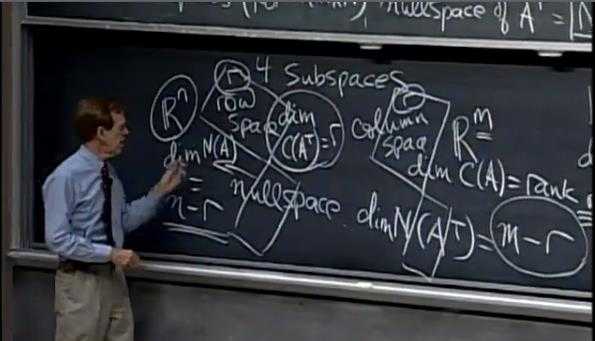
五、新型向量空间$M$
（1）定义：所有$3\times 3$矩阵 //将矩阵视为“向量”
（2）满足向量空间的八条运算法则：如对加法和数乘封闭等
（3）子空间：所有上三角矩阵、所有对称矩阵、所有对角矩阵$D$（前两者交集） //$D$的维数为3
标签：mat 图片 src row red inf line time style
原文地址：https://www.cnblogs.com/hg-love-dfc/p/10312008.html
