MT【288】必要性探路

标签：题意   图片   e^x   参考   jpg   nbsp   img   bsp   width   

已知$f(x)=e^x-\dfrac{1}{2}ax^2-b$
(1)当$a=1,b=1$时,求$f(x)$在$[-1,1]$上的值域.
(2)若对于任意实数$x$,$f(x)\ge0$恒成立,求$a+b$的最大值

解答:(1)略,(2)由题意$\dfrac{1}{2}ax^2+b\le e^x$,必要性:令$x=-\sqrt{2},a=-\dfrac{e^{-\sqrt{2}}}{\sqrt{2}}$则$a+b\le e^{-\sqrt{2}}$, 下证充分性
$f^{‘}(x)=e^x-ax=e^x+\dfrac{e^{-\sqrt{2}}}{\sqrt{2}}x$,显然$f(x)$在$-\sqrt{2}$处取到最小值.
故此时$f(x)\ge f(-\sqrt{2})=e^{-\sqrt{2}}-a-b=0$,即满足$f(x)\ge0$.

附参考答案：

MT【288】必要性探路

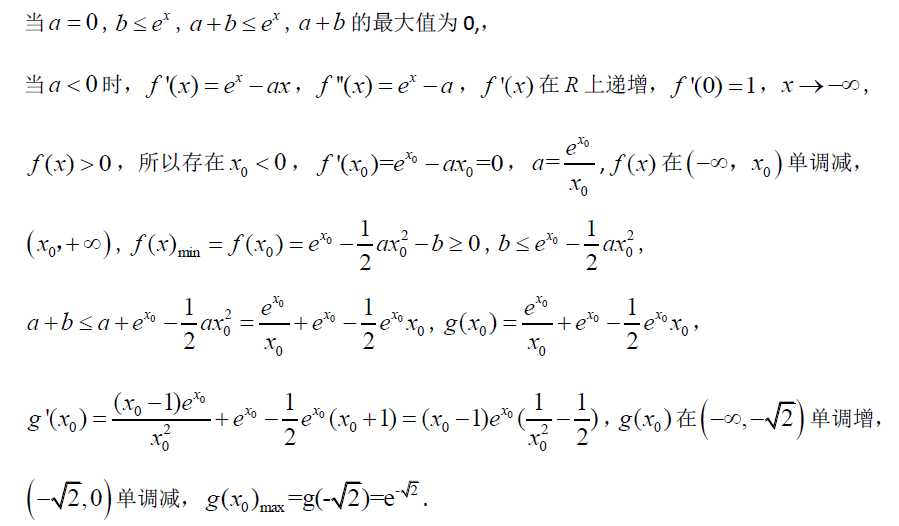
标签：题意   图片   e^x   参考   jpg   nbsp   img   bsp   width   

原文地址：https://www.cnblogs.com/mathstudy/p/10317860.html