标签：编号 image 通过 无法 相亲 将不 plog png 比较
0.思考一些一个分类问题：是否去相亲，LR解决的问题可能是这样的
在下面各个特征下给定w1，w2，w3，w4等参数值，将wx+b送到sigmoid函数中去，拿到一个概率p，我们在使用这个函数的时候会有一个损失函数loss function，对于这个代价函数通过GD梯度下降完成优化，拿到最好的w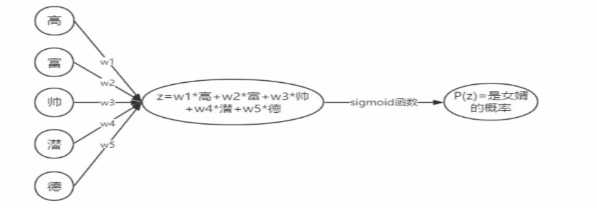
2.是否去相亲，有时候人更直观的方式是这样的。
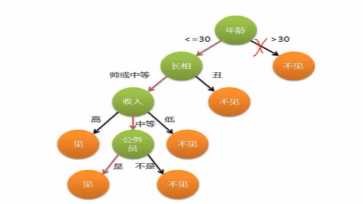
3.决策模型是模拟人类决策过程的思想的模型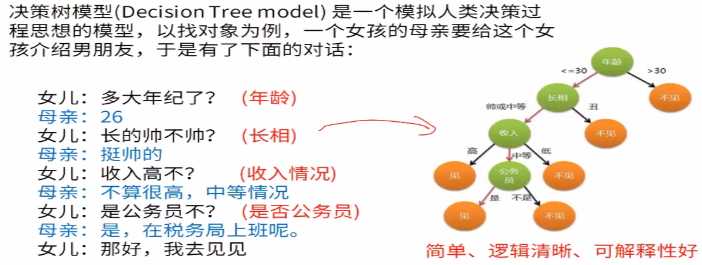
3.总体流程与核心问题
(1)决策树是基于“树”结构进行决策
每个“内部结点”对应于某个属性上的“测试”，内部结点对应于上图的绿色节点，针对某个条件做的判断，第一个绿色节点对年龄做了判断，第二个绿色节点对长相做了判断，第三个绿色节点对收入做了判断，最下面的绿色节点对公务员做了判断，每个分支对应于一种预测的结果，
每个分支节点对应于该测试的一种可能结果(即该属性的某个取值)
每个“叶节点”，对应于一个预测结果
(2)学习过程：
通过对训练样本的分析来确定“划分属性”(内部节点对应的属性)
(3)预测过程：将测试示例从根节点开始，沿着划分属性所构成的“判定测试序列”下行，直到叶节点
(4)总体流程：
“分而治之”(divide-and-conquer)
自根至叶的递归过程
在每个中间节点寻找一个“划分”(split or test)属性
(5)三种停止条件：
当前结点包含的样本全属于同一类别，无需划分
当前属性集为空，或者所有样本在所有属性上取值相同，无法划分
当前节点包含的样本集合为空，不能划分。
4.熵、信息增益、信息增益率
(1)熵：信息熵(entropy)是度量样本集合的“纯度”最常用的一种指标，假定当前样本集合D中第K类样本所占的比例为pk，则D的信息熵定义为：k是标签的种类个数，
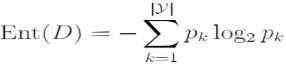
Ent(D)的值越小，则D的纯度越高，纯度最低，不确定度最高，Ent(D)越大，不纯度越高，在每个类别的比例一样的时候，取到的值是最大的 ，这个时候最不肯定，完全不知道自己摸出来的球是什么样的颜色。信息增益直接以信息熵为基础，计算当前划分对信息熵所造成的变化。计算信息熵时约定：若p=0，则plog2p=0，Ent(D)的最小值为0，最大值为log2|y|
为什么需要机器学习模型？机器学习模型是为了干什么？是为了做预估，提前预估出结果，如果模型做的足够好，就会把不确定度降得足够低。
5.最佳划分属性选择：信息增益
(1)信息增益(information gain):ID3中使用。
第v个分支的权重，样本越多越重要。
比如电商购物中有很多衣服的颜色，这些衣服的颜色分别是红、黄、蓝三色，机器学习模型是为了将不纯度降低，希望越来越纯。买衣服的小姐姐有的买了有的没有买，可以根据这个计算信息熵不确定性。可以根据颜色将衣服分为三份，每份都有一些样本，因为按照这个区进行区分了，所以肯定度有可能会变高。前面的Ent(D)是划分以前的信息熵，后面的是新分成的三份，每份中的不确定性，但是样本数减少了，所以要给这些进行一个加权，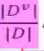
Dv是基于这种颜色来买衣服的人数，D是总共买衣服的人数
(2)信息增益示例：
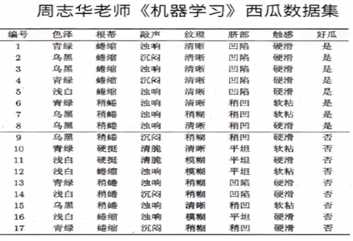
该数据集包含17个训练样例，结果有两个类别，|y|=2，其中正例占P1=8/17，反例占9/17。所以根节点的信息熵为：
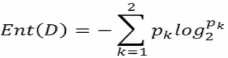
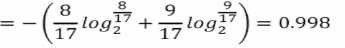
信息熵为0.998，说明不确定度比较高，不纯度比较高。
以属性“色泽”为例，其对应的3个数据子集分别为D1(色泽=青绿)，D2(色泽=乌黑)，D3(色泽=浅白)
子集D1包含编号为{1,4,6,10,13,17}的6个样例，其中正例占p1=3/6，反例占p2=3/6，D2，D3同理，3个节点的信息熵为：
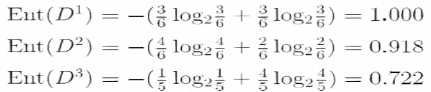
属性“色泽” 的信息增益为：
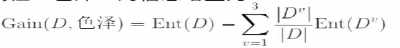
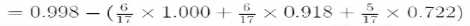=0.109,信息熵降低了0.109，后面一部分是划分之后的不纯度，基于颜色划分之后，计算得到的加权的不确定度。不确定度降低了0.109。
决策树朝着不确定度下降最多的方向去增长。
1.构建回归树
2.最优化回归树
1.采样与booststrap
2.bagging与随机森林
标签：编号 image 通过 无法 相亲 将不 plog png 比较
原文地址：https://www.cnblogs.com/bigdata-stone/p/10323135.html
