标签:分享 .com style man ble 分析 理论 递归 cost
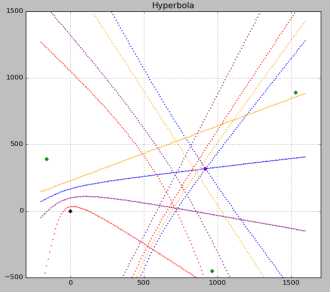
参考小区:黑点
其他小区:绿点
终端位置:红点
无误差模型双曲线:蓝线
测量粒度导致的误差:橘黄
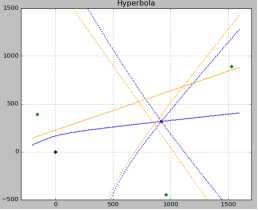
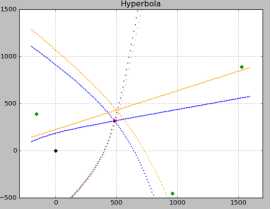
即小区能准确测量TA,但是TA的刻度就是16ts(对应单程距离4.88*16),所以就出现由度量刻度导致的误差。
上图中橘黄色曲线交点。
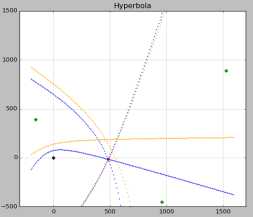
即小区测量的TA值会有波动,由测量波动导致的误差。
测量TA随机加1后的误差:紫色
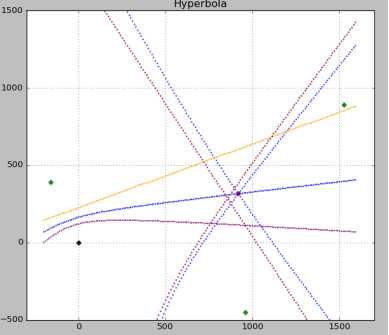
OTDOA模型假设终端到小区直线传播的距离差,而实际无线网络中,信号的传播很多是NLOS场景,所以在NLOS场景,TA的距离差不是模型假设的距离差,导致定位结果出现很大的误差。
将TA随机增长0-4个TA后的曲线交点:红色
《一种适用于NLOS环境的LTE终端迭代定位算法》中提到由NLOS引起的附加延时误差可根据COST259信道模型得到。一般情况下可以认为由NLOS引起的附加延时误差服从指数分布。
“Ti = Ti0 + ui + ni
Ti0是在LOS环境下的终端信号到达时间,ui是由检测系统造成的均值为0,标准差很小的高斯随机变量,ni表示由NLOS引起的附加延时误差。”
实际系统中,还有由于基站测量刻度导致的误差,比如基站上报以ta为单位,1ta=16ts,1个ts的距离是9.77米。且ui的波动也不是很小的随机变量。
一个点的画图分析不能代表全场景的,所以需要将基站小区和终端位置仿真,然后带入到假设的模型中,去评估模型的定位结果和模拟的终端位置的误差,以统计全局中的误差情况。
蜂窝网络中OTDOA定位误差仿真,场景模型:三个小区,小区间距500米,选择涂色部分进行模拟。
三种误差的CDF曲线及定位结果(绿色相对红色误差较小,整体误差见CDF):
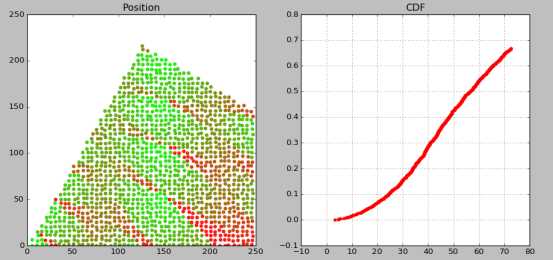
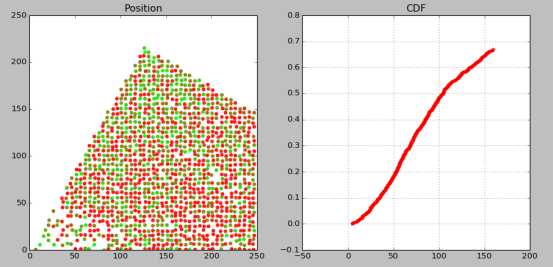
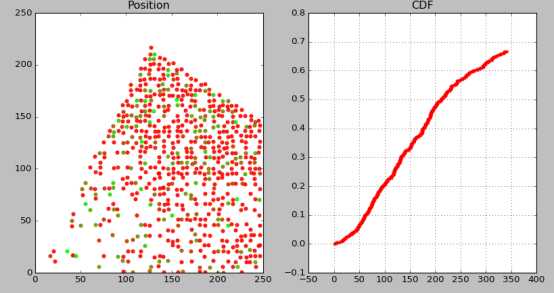
1TA误差是16*4.88
|
误差因素 |
平均误差(m) |
CDF 67%(m) |
CDF 95%(m) |
|
度量单位误差 |
64 |
72 |
136 |
|
测量波动(随机0~1个TA波动) |
354 |
159 |
985 |
|
NLOS(随机0~4个TA波动) |
589 |
340 |
1731 |
|
直接以小区位置定位 |
197 |
226 |
262 |
OTDOA的数学模型非常简单,但是实际无线网络环境及测量精度问题导致模型的误差比较大,定位精度不高。能否从误差分析的角度来证明或求取误差分布呢?
误差分析及传播
统计参数的误差统计模型=>定位结果的误差模型及评估
《蜂窝网络中基于TDOA的无线定位算法研究》
《LTE室内定位技术及优化方法研究》
https://blog.csdn.net/u012319493/article/details/80803034
Chan算法是非递归双曲线方程组解法,具有解析表达式解。其主要优点为在测量误差服从理想高斯分布时,它的定位精度高,计算量小,并且可以通过增加基站数量提高算法精度。该算法的前提是基于测量的误差为0均值高斯随机变量,对于实际环境中误差较大的测量值,比如NLOS环境下,该算法的性能会有显著下降。当基站数量大于3时,TDOA值得到非线性方程组个数要大于未知变量的个数,现将初始的TDOA方程组化为线性方程组,然后用加权最小二乘法得到初始解,再用第一次得到的初始解等约束变量进行第二次加权最小二乘估计,最后得到改进的位置估计。
该算法通过最小平方估计算出定位坐标,再与卡尔曼滤波器预定的定位坐标相比较,判断是否受NLOS影响,如果影响则抛弃,最后把接收的各组数据以不同的权重联合估计终端的位置。主要步骤如下:
数据分组处理
最小平方估计
卡尔曼预测
NLOS检测
数据联合估计更新
标签:分享 .com style man ble 分析 理论 递归 cost
原文地址:https://www.cnblogs.com/sunnypoem/p/10323685.html