梯度消失与梯度爆炸

标签：函数   tps   htm   http   div   高斯分布   一个   数值   计算   

https://blog.csdn.net/qq_25737169/article/details/78847691

产生消失的梯度问题的原因

先看一个极简单的深度神经网络：每一层都只有一个单一的神经元。如下图：

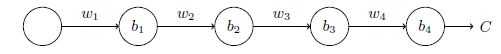
代价函数C对偏置b₁的偏导数的结果计算如下：

先看一下sigmoid 函数导数的图像：

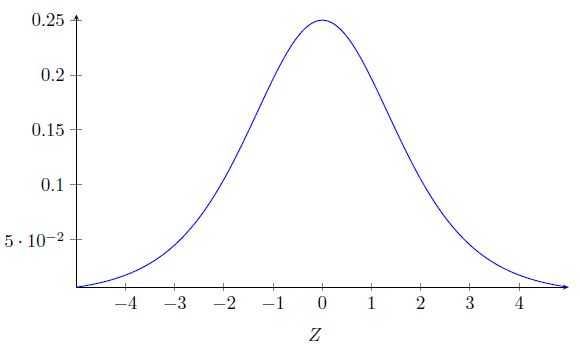
该导数在σ′(0) = 1/4时达到最高。现在，如果我们使用标准方法来初始化网络中的权重，那么会使用一个均值为0 标准差为1 的高斯分布。因此所有的权重通常会满足|w_j|<1。从而有w_jσ′(z_j) < 1/4。

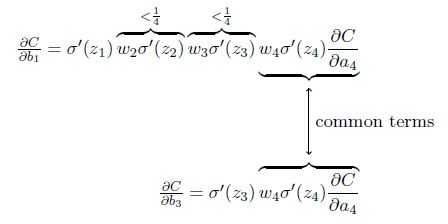
这其实就是消失的梯度出现的本质原因了。

可以考虑将权重初始化大一点的值，但这可能又会造成激增的梯度问题。

根本的问题其实并非是消失的梯度问题或者激增的梯度问题，而是在前面的层上的梯度是来自后面的层上项的乘积。所以神经网络非常不稳定。唯一可能的情况是以上的连续乘积刚好平衡大约等于1，但是这种几率非常小。

所以只要是sigmoid函数的神经网络都会造成梯度更新的时候极其不稳定，产生梯度消失或者激增问题。

解决梯度消失问题

梯度消失与梯度爆炸

标签：函数   tps   htm   http   div   高斯分布   一个   数值   计算   

原文地址：https://www.cnblogs.com/fpzs/p/10327294.html