标签:inf 特征 删掉 部分 记录 合法性 最大的 com 选择
PKU:
机试:
d1t1:
考虑拓扑序的合法性,每个点的入边必须先加入。f[S]表示先出来的是S集合的点,对应边的方案数。加入x的时候,把入边方向确定,出边自然后面会确定的
2^n*n
d1t2:
虚树,点数=边数+1,NTT,
先咕咕咕
d1t3:
地主斗。。。
炸弹,火箭先处理
剩下牌的特征值(每个方式最大的),以及对应的牌数
hash表存一下
然后再找B的
特征值要状压,还要边加入边计算特征值。
d2t1:
a[i]=0的部分分:
分成n段
每个点在每个段的方案数有相同之处
f[i][j]表示前i个,第i个取再前j段的前缀和
转移的时候
枚举最左边选择j的l
l到i的部分就是盒子放球的问题
据说是APIO赛艇弱化版0?
满分:
区间dp
dp[i][l][r],前i高位,确定了[l],[r]方案数
还要什么数位dp记录0/1
咕咕咕咕
d2t2:
两个环有公共边,
一定在一个SCC里
反之,可能八字图情况,在SCC里,却没有公共边
先求出SCC
再在SCC中求出点双连通分量个数,和就是ans
SCC中不是V-DCC的环坑定没有公共边
SCC中的V-DCC一定还是SCC
而且没有上面的情况了
所以就是一个联通块
d2t3
每个圆被完全覆盖就可以删掉
n^2*m部分分
两种方法:
①圆的面积并
②对于i,找到最左最右的圆和i的交的角度
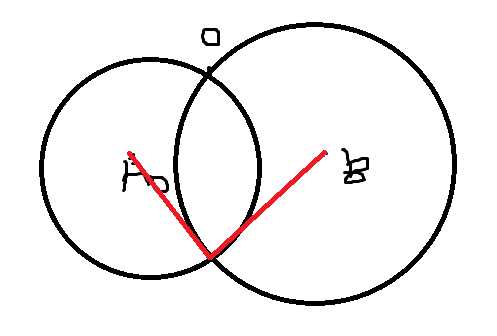
记录红色角的最大值
左边同理
如果角相互有覆盖,A0就被覆盖了
发现所有剩下的点
都在{A0,A1,,,An,O}组成的凸包上
O是变化的
对于{Ai}先建立凸包
每个O,二分包住的部分删掉。
O(nlogn+mlogn)
标签:inf 特征 删掉 部分 记录 合法性 最大的 com 选择
原文地址:https://www.cnblogs.com/Miracevin/p/10327637.html