标签:积分 微积分 targe 要求 形状 auto ons .com bilibili
在只考虑重力的作用的情况下,一质点从点A沿某条曲线到点B,问怎样的曲线能使所需时间最短?
这一问题被称为最速降线问题(Brachistochrone),由约翰·伯努利在1696年提出来挑战欧洲的数学家。
约翰·伯努利的证明实际上非常巧妙,利用了费马原理:一束光从A点传播到B点总是沿着尽可能快的路径。
从费马原理实际上可导出斯涅耳定理(Snell’s Law):考虑光线跟一条垂直两介质边界所成的角度,该角度的正弦值除以光速在从一种介质转移到另一种介质时保持不变。
$$\dfrac{\sin(\theta_1)}{v_{\text{air}}} = \dfrac{\sin(\theta_2)}{v_{\text{water}}}$$

光的传播
因此原问题可以想象为一束光在不同折射率的介质中传播,即以不同的速度连续的沿着滑道向下走:

当层数不断增加,我们就得到了想要的路径。
由能量守恒定律,重力势能转化为动能,因此:
$$v = \sqrt{2gy}$$
又根据斯涅尔定理可得:
$$\dfrac{\sin(\theta)}{\sqrt{y}} = \text{constant(常数)}$$
这就是我们要求的曲线方程。
这一曲线方程实际上就是旋轮线,即滚动的轮子边缘上的一点所描述的形状。
圆上定点P,圆与水平线的切点为C,圆滚动时,点C充当点P的瞬时旋转中心:
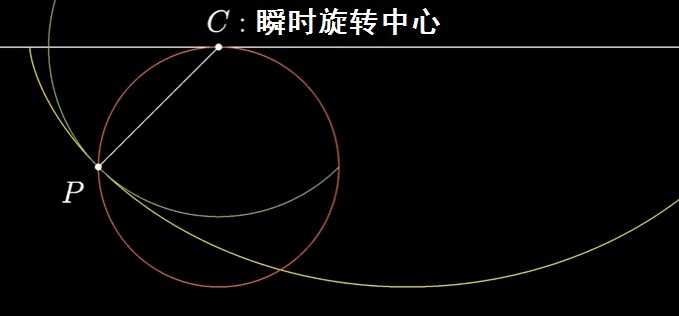
所以CP垂直于摆线过点P的切线,又因直角圆周角对应直径,所以该切线一定过圆的最低点,交点与C的连线即为圆的直径:
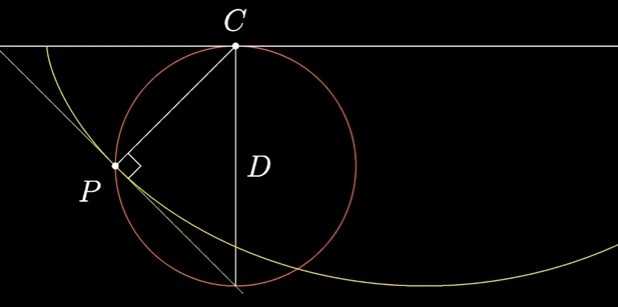
设直线与切线的夹角为$\theta$,根据相似三角形,我们可以计算出点P到水平线的距离:
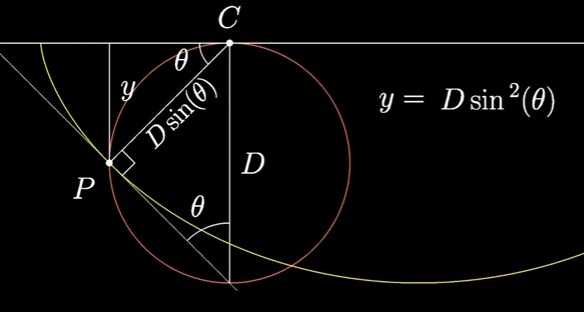
即
$$\dfrac{\sin(\theta)}{\sqrt{y}} = \dfrac{1}{\sqrt{D}} = \text{constant(常数)}$$
由此证明最速降线实际就是摆线。
从微积分的方法考虑这一问题,设曲线方程为$y=y(x)$,速度与纵坐标有$v=\sqrt{2gy}$的关系,同时
$$v = \dfrac{ds}{dt} = \sqrt{1+y‘^2} \dfrac{dx}{dt}$$
其中$s$表示曲线的弧长,$t$表示时间,于是
$$dt = \dfrac{\sqrt{1+y‘^2}}{v}dx = \dfrac{\sqrt{1+y‘^2}}{\sqrt{2gy}}dx$$
所以从A到B的时间为
$$t = J(y) = \int_A^B \dfrac{\sqrt{1+y‘^2}}{\sqrt{2gy}}dx$$
这样时间$t$被写成了关于$y$的泛函,而求时间最短问题变成了在满足边界条件
$$y(A) = 0, y(B) = y_B$$
下的对泛函$J(y)$求极值问题,即变分问题。
考虑对泛函$$J(y) = \int_b^a F(x,y,y‘)dx$$变分
$$\begin{aligned}
\delta J(y) &= J(y+\delta y) - J(y) \\
&= \int_a^b \left[\dfrac{\partial F}{\partial y}\delta y + \dfrac{\partial F}{\partial y‘}\delta y‘\right]dx \\
&= \int_a^b \left[\dfrac{\partial F}{\partial y} - \dfrac{d}{dx}\left(\dfrac{\partial F}{\partial y‘}\right) \right] \delta y dx
\end{aligned}$$
令$\delta J(y) = 0$即得
$$\dfrac{\partial F}{\partial y} - \dfrac{d}{dx}\left(\dfrac{\partial F}{\partial y‘}\right) = 0$$
将上述方程带入,即将变分问题转化为微分方程问题,解此微分方程即得所求曲线。
参考链接:
标签:积分 微积分 targe 要求 形状 auto ons .com bilibili
原文地址:https://www.cnblogs.com/lfri/p/10327570.html