图像识别的一些基础

标签：under   图片   idt   积分   特定   abc   一个   灰度   图像   

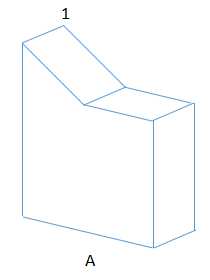
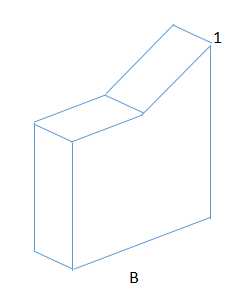
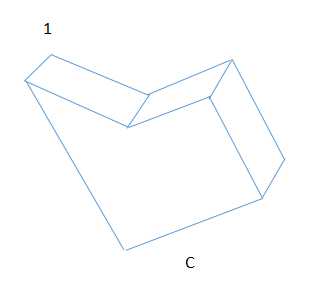
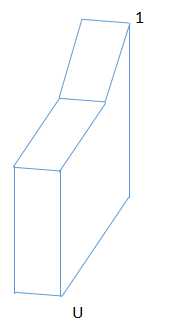
以上是四副正射影像图，提取好边线，对于每个角点，能自动匹配标记好号码1~n；

*在距离物体的距离，大于物体的2.5倍，那么，就可以忽略物体的透视，认为得到物体的影像是正射影像；

已知ABC是同一物体的正射影像，而U是同类物体，但不一定是同一物体的正射影像。

对于各个点，有：

X_U1 = aX_A1 + bX_B1 + cX_C1 + d

X_U2 = aX_A2 + bX_B2 + cX_C2 + d

X_U3 = aX_A3 + bX_B3 + cX_C3 + d 

X_U4 = aX_A4 + bX_B4 + cX_C4 + d 

*想在一下，只有旋转没有平移的平面旋转 Xt = A Xs ，A是2*2的矩阵，Xt是XY

以上可以化为矩阵的形式，解出a,b,c,d;

X_U1 X_A1  X_B1  X_C1  1  　　　 a

X_U2    =   X_A2  X_B2  X_C2  1 　　　  b　　　　　　　

X_U3　　  X_A3  X_B3  X_C3  1　　　   c

X_U4 　　 X_A4  X_B4  X_C4  1              d

那么，可以预测U5，如果U5预测的位置和标记出的位置不相同，那就有理由相信，U5和ABC中的物体，不是同一个物体；

另一种识别的办法，就是用信号的原理，求积分：

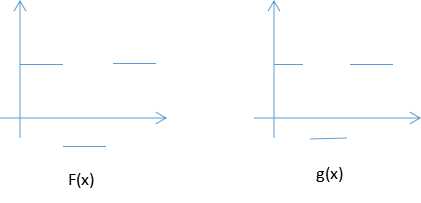
对于信号函数，假如f(x)g(x)在X0处同号，那就取得很大的值如果有:

∫F(x)g1(x)dx，∫F(x)g2(x)dx……

取得最大只者，F(x)和g(x)最相似；

假如人脸的图像，都规定缩放在一个特定的尺寸，而且先进行二值化处理；

然后逐个像素两两相乘，得出最大者；

或者对两幅图像建模，灰度函数也可：

∫_D f(x,y)g(x,y)dxdy

图像识别的一些基础

标签：under   图片   idt   积分   特定   abc   一个   灰度   图像   

原文地址：https://www.cnblogs.com/pylblog/p/10329510.html