标签:左右子树 逻辑 使用 树的遍历 java 创建 color 分享图片 evel
1 // 看二分搜索树中是否包含元素e 2 public boolean contains(E e){ 3 return contains(root, e); 4 } 5 6 // 看以node为根的二分搜索树中是否包含元素e, 递归算法 7 private boolean contains(Node node, E e){ 8 9 if(node == null) 10 return false; 11 12 if(e.compareTo(node.e) == 0) 13 return true; 14 else if(e.compareTo(node.e) < 0) 15 return contains(node.left, e); 16 else // e.compareTo(node.e) > 0 17 return contains(node.right, e); 18 }
二分搜索树的遍历操作,遍历操作就是把所有节点都访问一遍
前序遍历:先访问节点,在访问左右子树。
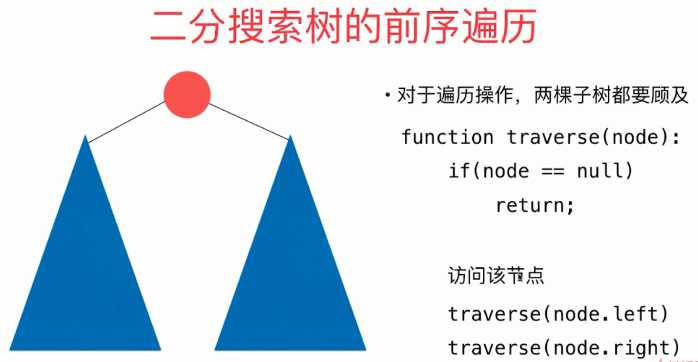
递归代码:先写递归终止条件,再写递归组成逻辑
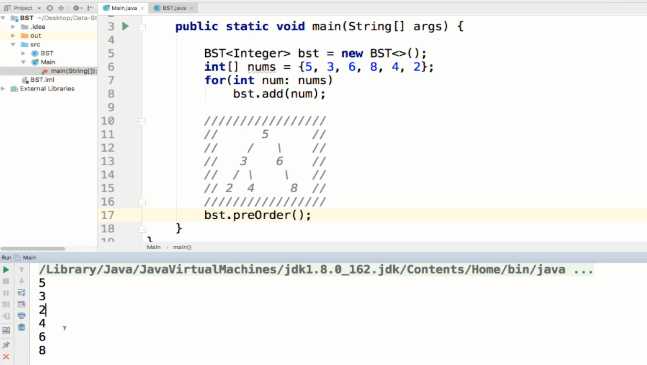
1 // 二分搜索树的前序遍历 2 public void preOrder(){ 3 preOrder(root); 4 } 5 6 // 前序遍历以node为根的二分搜索树, 递归算法 7 private void preOrder(Node node){ 8 if(node == null) //递归终止条件 9 return; 10 11 System.out.println(node.e); 12 preOrder(node.left); //递归组成逻辑 13 preOrder(node.right); 14 }
6-7 二分搜索树的中序遍历和后序遍历

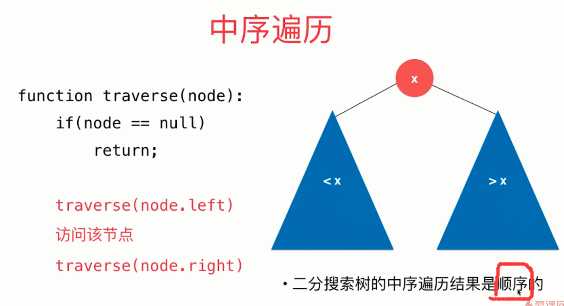
1 // 二分搜索树的中序遍历 2 public void inOrder() { 3 inOrder(root); 4 } 5 6 // 中序遍历以node为根的二分搜索树,递归算法 7 private void inOrder(Node node) { 8 9 if (node == null) { 10 return; 11 } 12 13 inOrder(node.left); 14 System.out.print(node.e); 15 inOrder(node.right); 16 17 }


1 // 二分搜索树的后序遍历 2 public void postOrder() { 3 postOrder(root); 4 } 5 6 // 后序遍历以node为根的二分搜索树,递归算法 7 private void postOrder(Node node) { 8 9 if (node == null) { 10 return; 11 } 12 postOrder(node.left); 13 postOrder(node.right); 14 System.out.print(node.e); 15 16 }
6-9 二分搜索树前序遍历的非递归实现
//结合视频、PDF看这段代码
1 // 二分搜索树的非递归前序遍历 2 public void preOrderNR(){ 3 4 Stack<Node> stack = new Stack<>();//stack使用泛型型,里面装的是Node类对象 5 stack.push(root); //入栈,向根节点中添加root 6 while(!stack.isEmpty()){ 7 Node cur = stack.pop(); //把栈顶元素来出来,放进cur中,cur节点就是我们当前要访问的节点 8 System.out.println(cur.e); 9 10 if(cur.right != null) //前序遍历顺序:根→left节点→right节点,由于栈是后入先出的,所以right节点先入栈,left节点后入栈 11 stack.push(cur.right); 12 if(cur.left != null) 13 stack.push(cur.left); 14 } 15 }
1 // 二分搜索树的层序遍历 2 public void levelOrder(){ 3 4 Queue<Node> q = new LinkedList<>();//对于层序遍历来说,需要使用一个队列,这里使用Java自带的Queue(导入包Queue),不过Java的Queue本质是一个接口,真正实现它是时候需要实现一个具体的底层数据结构,选择使用链表的方式来实现(导入包LinkedList)。 5 q.add(root); 6 while(!q.isEmpty()){ 7 Node cur = q.remove();//队列中的元素出队之后的那个元素就是我们当前要访问的元素 8 System.out.println(cur.e); 9 10 if(cur.left != null) 11 q.add(cur.left); 12 if(cur.right != null) 13 q.add(cur.right); 14 } 15 }
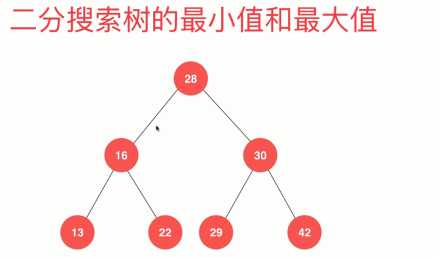
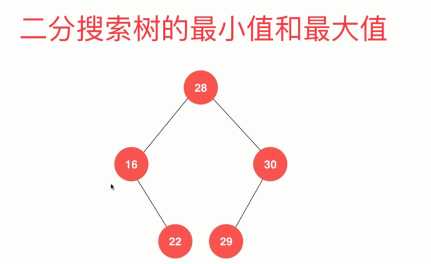
对应图,一定是从根节点开始不停的向左走、向右走,走不动了,就找到最小、最大值。
1 // 寻找二分搜索树的最小元素 2 public E minimum(){ 3 if(size == 0) 4 throw new IllegalArgumentException("BST is empty"); 5 6 Node minNode = minimum(root); //maximum(root):以root为根的二分搜索树的最小值 7 return minNode.e;//返回以root为根的二分搜索树的最小元素值 8 } 9 10 // 返回以node为根的二分搜索树的最小值所在的节点 11 private Node minimum(Node node){ 12 if( node.left == null )//向左走走不动了 13 return node; 14 15 return minimum(node.left);//如果不满足if条件,执行这一步 16 } 17 18 // 寻找二分搜索树的最大元素 19 public E maximum(){ 20 if(size == 0) 21 throw new IllegalArgumentException("BST is empty"); 22 23 return maximum(root).e; 24 } 25 26 // 返回以node为根的二分搜索树的最大值所在的节点 27 private Node maximum(Node node){ 28 if( node.right == null ) 29 return node; 30 31 return maximum(node.right); 32 }
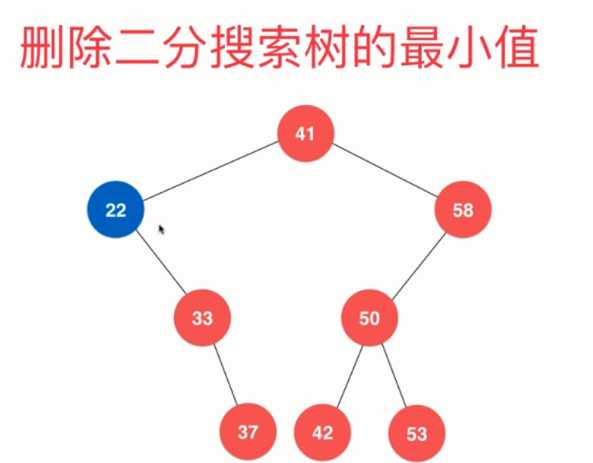 变成
变成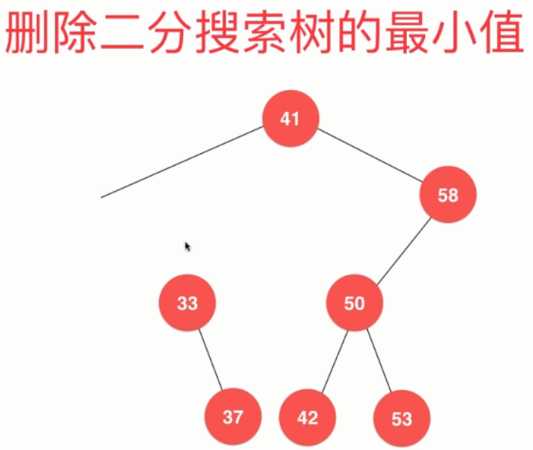 变成
变成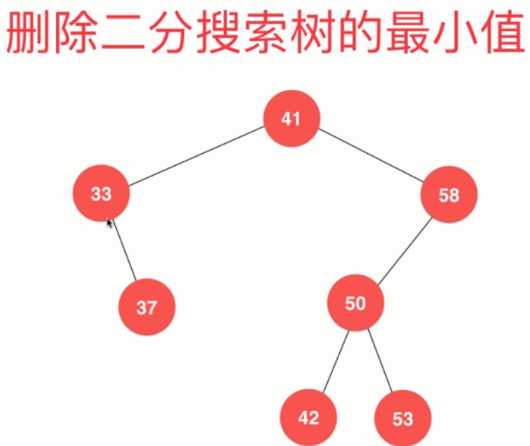
1 // 从二分搜索树中删除最小值所在节点, 返回最小值 2 public E removeMin(){ 3 E ret = minimum(); 4 root = removeMin(root);//从root开始尝试删除最小值所在节点 5 return ret; 6 } 7 8 // 删除掉以node为根的二分搜索树中的最小节点 9 // 返回删除节点后新的二分搜索树的根 10 private Node removeMin(Node node){ 11 12 if(node.left == null){ //不能向左走了,当前节点node就是最小值所在节点,要删到这个节点 13 Node rightNode = node.right;//要删的这个当前节点可能是有右子树的,右子树不能丢。 创建rightNode,保存当前节点的右子树 14 node.right = null;//对将要删除的节点让它的right等于空,也就是将要删除的node节点从二叉树中脱离。 15 size --;//删除掉了一个元素,整体size要-- 16 return rightNode;//返回rightNode,起到删除最小值所在节点的作用。把node删除,当前二分搜索树的根就是node的右孩子:node.right( rightNode ) 17 } 18 19 node.left = removeMin(node.left);//如果没有递归到底,不满足if条件,说明node还有左孩子,要做的是:去删除掉到node左子树对应的最小值 20 return node;//删除掉到node左子树对应的最小值后,对于当前以node为根的二分搜索树,它的根节点依然是node,将它返回 21 } 22 23 // 从二分搜索树中删除最大值所在节点 24 public E removeMax(){ 25 E ret = maximum(); 26 root = removeMax(root); 27 return ret; 28 } 29 30 // 删除掉以node为根的二分搜索树中的最大节点 31 // 返回删除节点后新的二分搜索树的根 32 private Node removeMax(Node node){ 33 34 if(node.right == null){ 35 Node leftNode = node.left; 36 node.left = null; 37 size --; 38 return leftNode; 39 } 40 41 node.right = removeMax(node.right); 42 return node; 43 }
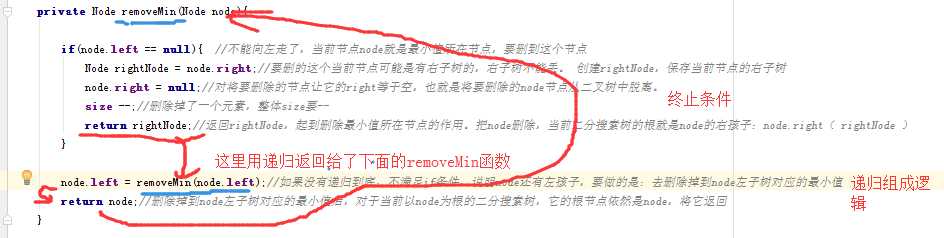
看下面这个图便于理解

6-12 删除二分搜索树的任意元素
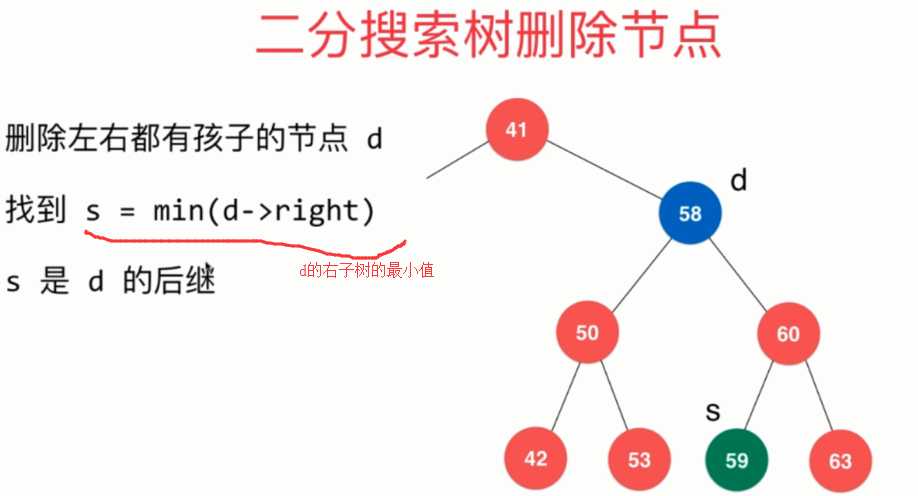
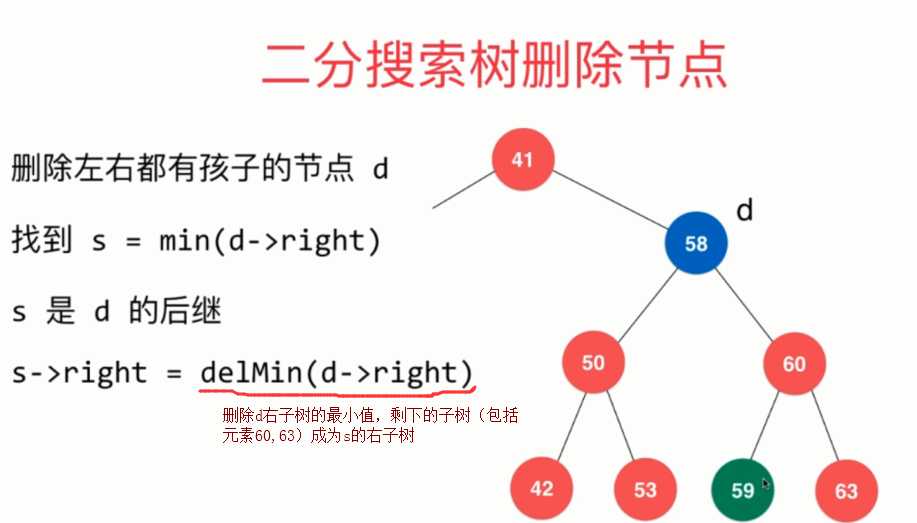 即
即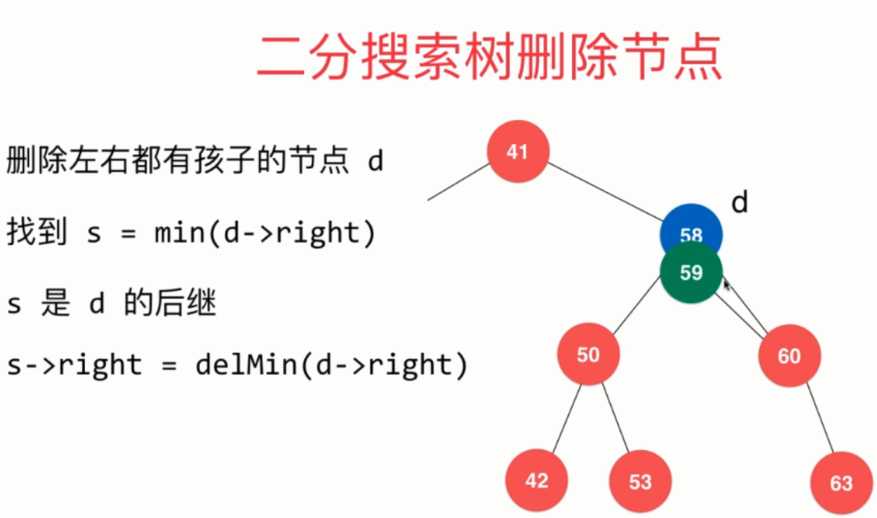
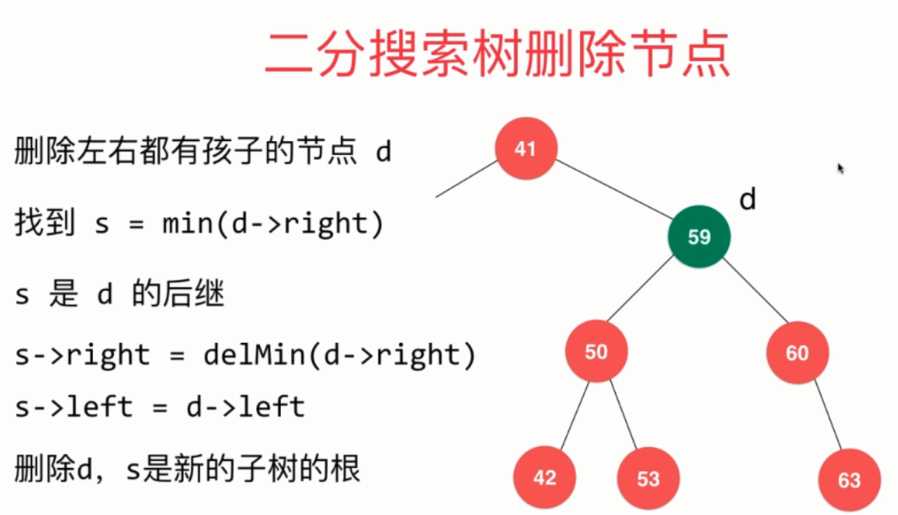
具体实现代码:
1 // 从二分搜索树中删除元素为e的节点 2 public void remove(E e){ 3 root = remove(root, e); 4 } 5 6 // 删除掉以node为根的二分搜索树中值为e的节点, 递归算法 7 // 返回删除节点后新的二分搜索树的根 8 Node remove(Node node, E e){ 9 10 if( node == null ) 11 return null; 12 13 if( e.compareTo(node.e) < 0 ){ 14 node.left = remove(node.left , e); //到node的左子树中尝试删除e 15 return node; 16 } 17 else if(e.compareTo(node.e) > 0 ){ 18 node.right = remove(node.right, e); 19 return node; 20 } 21 else{ // e.compareTo(node.e) == 0代删除的e和当前节点的e相等 22 23 // 待删除节点左子树为空的情况 24 if(node.left == null){ 25 Node rightNode = node.right; 26 node.right = null; 27 size --; 28 return rightNode; 29 } 30 31 // 待删除节点右子树为空的情况 32 if(node.right == null){ 33 Node leftNode = node.left; 34 node.left = null; 35 size --; 36 return leftNode; 37 } 38 39 // 待删除节点左右子树均不为空的情况 40 41 // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点 42 // 用这个节点顶替待删除节点的位置 43 Node successor = minimum(node.right); 44 size ++; 45 46 successor.right = removeMin(node.right); 47 successor.left = node.left; 48 49 node.left = node.right = null; 50 size --; 51 52 return successor; 53 }
标签:左右子树 逻辑 使用 树的遍历 java 创建 color 分享图片 evel
原文地址:https://www.cnblogs.com/make-big-money/p/10333564.html