标签：其他   变形   统计   memset   引入   idg   二分答案   space   comment   

浅谈状压dp

小蒟蒻的第一篇博客

一、问题引入(链接)

农场主约翰新买了一块长方形的新牧场，这块牧场被划分成M行N列(1 ≤ M ≤ 12; 1 ≤ N ≤ 12)，每一格都是一块正方形的土地。约翰打算在牧场上的某几格里种上美味的草，供他的奶牛们享用。

遗憾的是，有些土地相当贫瘠，不能用来种草。并且，奶牛们喜欢独占一块草地的感觉，于是约翰不会选择两块相邻的土地，也就是说，没有哪两块草地有公共边。

约翰想知道，如果不考虑草地的总块数，那么，一共有多少种种植方案可供他选择？（当然，把新牧场完全荒废也是一种方案）

首先，看到这个问题的数据范围，我立马想到了搜索，但O(2^(m*n))的时间复杂度根本无法接受，怎么办呢？看看这篇文章的题目，状压dp！

我们先来看转移方程式，dp[i][S]+=dp[i-1][S‘]，其中，S为一个集合，i表示处于哪一行，S包含了当前这一行放了奶牛的点，显然，这个方程是没有后效性并且满足最优子结构性的，可关键就在于这个集合S如何表示。

我们发现，对于每一个点，只有两种情况，放牛或是不放牛，这两种情况可以用0和1来表示，0表示不放，1表示放，于是这个S就被我们表示为了一个01串，而这个串我们可以看做是一个二进制数，于是这个集合S就成功的被我们用一个数表示出来了，这个过程可以形象的看做吧一个集合压缩，于是状压dp因此而得名。

二、预备知识(大佬可以直接跳过)

位运算是一类速度极快的基本运算，包括位移、与、或、非、异或运算，是基于二进制的运算。

1. 左移:符号‘<<‘,可以形象地理解为把一个二进制数向左移了几位，如：110010<<2=11001000,在十进制上体现为移一位，就乘一个2，如:5<<2=20

2. 右移，符号‘>>‘，相当于移一位，除以一个2，如：110010>>2=1100,9>>2=2;

3. 与，符号‘&‘,两位上同为1就为1，否则为0，如：101&110=100

4. 或，符号‘|‘,两位上任一位为1,就为1，否则为0，如：101|100=101

5. 非，符号‘~‘,按位取反，如：~100=011

6. 异或，符号‘^‘，两位上相同为1，不同为0，如：100^101=001

   (注意，不要把左移和和右移搞反了，还有位运算的优先级是最低的即1<<(a-1)=1<<a-1)

7. 实际运用：

   以上一题为例，判断S第i位是否为0：S&(1<<(i-1))

   将第i位设置为1：S|(1<<i-1)

   将第i位设置为0：S&~(1<<i-1)

   不明白的自己举几个例子模拟一下我懒得讲了

三、代码实现

#include<cstdio>
#define N 13
#define M 1<<12
#define mod 100000000 
int dp[N][M],n,ans,m,a[N];
//a[i]表示第i行的草地情况,用一个二进制数来表示 
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    { 
        int x;
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&x);
            a[i]<<=1;
            if(!x) a[i]++;
            //这里用1来表示贫瘠的土地，方便后面判断 
        }
    }
    for(int i=0;i<1<<m;i++)
    //因为第一行无法被上一行影响，所以说要先单独处理 
    if(!(i&a[1]) && !((i<<1)&i)) dp[1][i]=1; 
    //若牛都是放在肥沃的草地上的并且牛不相邻 
    //不明白的手动模拟一下
    for(int i=2;i<=n;i++)//枚举层数 
    for(int j=0;j<1<<m;j++)//枚举第i层的状态 
    if(!(a[i]&j) && !((j<<1)&j)) 
    //判断j是否合法
    for(int k=0;k<1<<m;k++)//枚举第i-1层的状态 
    if(!(a[i-1]&k) && !((k<<1)&k) && !(j&k))
    //若j和k是合法的 
    dp[i][j]+=dp[i-1][k],dp[i][j]%=mod;
    for(int i=0;i<1<<m;i++)
    if(!(a[n]&i)) 
    ans+=dp[n][i],ans%=mod;
    //最后将最后一层的方案数都统计起来 
    printf("%d",ans);//愉快输出答案 
}

四、更多例题

(1)炮兵阵地

司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：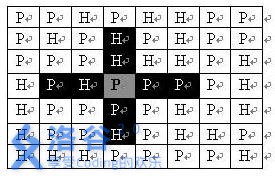 

如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。(1<=N<=100,1<=M<=10)

分析

与上一道题差不多，只不过炮兵的影响范围变成了2格而已，于是我们尝试写出dp方程式：dp[i][S]=..........

等一等，这个方程怎么也写不出来，因为你这一行的最优解是由上两行转移过来的，而你无法确定上一行和转移来往上第二行的往上第三行是否与上一行冲突，好绕。

那怎么办？再加一维呀！dp[i][S1][S2] 表示第i行上两行的状态分别为S1和S2的最大放兵数，于是得到方程：

dp[i][S1][S2]=max(dp[i-1][S2][S3]+cnt[S1]

等一等，这个方程要枚举三个状态，时间复杂度为O((2^M)^3*N),将N=100，M=10代入，复杂度高达O(10^11) 稳妥妥的超时

怎么办？我们发现，枚举的三个状态中有太多无用的了，于是我们可以先将可用的状态预处理出来，经计算，最多有不超过70个有用状态，于是时间复杂度大大降低，便可以过了！

代码

#include<cstdio>
#include<iostream>
#include<algorithm>
#define N 105
#define M 70
using namespace std;
int dp[N][M][M],s[N][M],cnt[N][M];
//s[i]用来存第i行有效的状态，s[i][0]存个数 
//cnt[i][j]表示第i行第j个有用的状态所包含的炮兵数 
int n,ans,m;
int cal(int x)//计算状态x含有几个炮兵 
{
    int a=m,num=0;
    while(a--)
    {
        if(x&1) num++;
        x>>=1;
    }
    return num;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int t=0;
        for(int j=1;j<=m;j++)
        {
            char ch;
            cin>>ch;
            t<<=1;
            if(ch==‘H‘) t++;
            //将地图压缩成一个数方便后面判断 
        }
        for(int j=0;j<1<<m;j++)
        if(!(t&j) && !((j<<1)&j) && !((j<<2)&j))
        //判断状态是否有用 
        s[i][++s[i][0]]=j,cnt[i][s[i][0]]=cal(j);
        //用s[i][0]存第i行可行状态的数量并计算当前状态炮兵数 
    }
    //单独处理第一行 
    for(int i=1;i<=s[1][0];i++)//枚举第一行状态 
    dp[1][i][0]=cnt[1][i];
    //单独处理第二行 
    for(int i=1;i<=s[2][0];i++//枚举第2行状态 
    for(int j=1;j<=s[1][0];j++)//枚举第1行状态 
    if(!(s[2][i]&s[1][j]))
    dp[2][i][j]=max(dp[2][i][j],dp[1][j][0]+cnt[2][i]);
    //批量处理第3~i行 
    for(int i=3;i<=n;i++)//枚举行 
    for(int j=1;j<=s[i][0];j++)//枚举当前行状态 
    for(int k=1;k<=s[i-1][0];k++)//枚举上一行状态 
    if(!(s[i][j]&s[i-1][k]))
    for(int l=1;l<=s[i-2][0];l++)//枚举往上第二行的状态 
    if(!(s[i-1][k]&s[i-2][l]) && !(s[i][j]&s[i-2][l]))
    dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][l]+cnt[i][j]);
    //枚举最终状态取最大值 
    for(int i=1;i<=s[n][0];i++)
    for(int j=1;j<=s[n-1][0];j++)
    if(!(s[n][i]&s[n-1][j]))
    ans=max(ans,dp[n][i][j]);
    printf("%d",ans);//愉快输出 
}

售货员的难题

某乡有nn个村庄(1<n≤20)，有一个售货员，他要到各个村庄去售货，各村庄之间的路程s(0<s<1000)是已知的，且A村到B村与B村到A村的路大多不同。为了提高效率，他从商店出发到每个村庄一次，然后返回商店所在的村，假设商店所在的村庄为1，他不知道选择什么样的路线才能使所走的路程最短。请你帮他选择一条最短的路。

分析

这是一道经典的TSP问题(不懂得自己去查),我们定义dp[i][S]当前售货员走到了i村，走过了S村(S为走过的村子的集合），因此很容易写出方程式：

dp[i][S]=min(dp[j][S‘]+dis[i][j])其中S=S‘+i

由于售货员最后还要回到1村，因此最终ans=min(dp[i][S_all]+dis[i][1])

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#define inf 0x3f3f3f3f//定义正无穷为一个极大极大的数 
using namespace std;
int dis[21][21]; 
int n,ans=inf;
int dp[21][1<<20];
int main()
{
    scanf("%d",&n);
    memset(dp,inf,sizeof(dp));//初始化为正无穷 
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    scanf("%d",&dis[i][j]);
    dp[1][1]=0;//初始化边界条件，因为最开始从1村出发 
    for(int i=0;i<1<<n;i++)//枚举当前状态 
    for(int j=1;j<=n;j++)//枚举当前所在的点 
    if(i&(1<<j-1))//若j包含在i里面 
    for(int k=1;k<=n;k++)
    if(!(i&(1<<k-1)))//若k不包含在i里面，即k没有走过 
    dp[k][i|(1<<k-1)]=min(dp[k][i|(1<<k-1)],dp[j][i]+dis[j][k]);
    //i|(1<<k-1)即为将i的第k位设置为1，因为我即将要走这个点 
    for(int i=1;i<=n;i++)
    ans=min(ans,dp[i][(1<<n)-1]+dis[i][1]);//寻找最终答案 
    printf("%d",ans);//愉快输出 
}

可数据太强，无论如何都只拿得到90分，如何优化的问题就留给读者思考

其实只是作者太蒟了写不来

(3)Travelling

题目翻译：ACMer先生想去度假，有n个城市，m条无向边，ACMer先生想要走遍所有的城市，他可以从任何一个点出发，因为超人在最开始的时候可以把他带到任何城市但只有一次(原题上写的就是超人!!!)，但ACMer先生是一个容易感到无聊的人，因此他不希望重复走一个城市超过两次，求他这次旅行所需要走过的最短距离。

输入：有很多组输入数据，对于每组输入数据，第一行两个整数n,m,代表城市和边的数量(1<=n<=10),接下来m行，每行三个整数a,b,c,表示a城市和b城市之间存在一条长度为c的路径。

输出：对于每组输入数据，输出一个整数，代表走过这n个城市的最短路径。

样例输入：

2 1

1 2 100

3 2

1 2 40

2 3 50

3 3

1 2 3

1 3 4

2 3 10

样例输出：

100

90

7

分析

这也是一道经典的TSP问题，相对于上一道题只不过多了一点———一个城市最多可以走过两次，既然我们可以把一个状态压缩成一个二进制数，我们也可以将其压缩为一个三进制数，用0表示当前城市没有走过，1表示走过一次，2表示走过了两次，然后就可以愉快地转移了！详情见代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#define N 11
#define M 60000
#define inf 0x3f3f3f3f
using namespace std;
int dis[N][N],f[N][M],power[11];
//f[i][S]表示走到了i号点，已经走过的集合为S的最短距离
//power[i]=3^i 
int n,m,ans;
inline int check(int x)//判断状态x是否把每个城市都走过了 
{
    int cnt=n;
    while(cnt--)
    {
        if(x%3==0) return 0;
        //若当前位上是0，说明这个城市还没有走过 
        x/=3;
    }
    return 1;
}
int main()
{
    power[0]=1;
    for(int i=1;i<=10;i++)
    power[i]=power[i-1]*3;//预处理出3^n 
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        memset(dis,inf,sizeof(dis));
        memset(f,inf,sizeof(f));
        ans=inf;
        while(m--)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            dis[a][b]=min(dis[a][b],c);//数据比较毒瘤 
            dis[b][a]=dis[a][b];
        }
        for(int i=1;i<=n;i++)
        f[i][power[i-1]]=0;
        //枚举出发点，初始化边界条件 
        for(int i=0;i<power[n];i++)//枚举状态 
        {
            for(int j=1;j<=n;j++)//枚举之前到过的点 
            if((i/power[j-1])%3!=0)//判断这个点之前是否到过 
            for(int k=1;k<=n;k++)
            {
                if((i/power[k-1])%3!=2&&k!=j)//若k号点只到过1次或0次
                //那么还可以走一次 
                f[k][i+power[k-1]]=min(f[k][i+power[k-1]],f[j][i]+dis[j][k]);
                //更新 
            }
        }
        for(int i=1;i<power[n];i++)//枚举状态 
        if(check(i)) //判断是否把所有城市都走了个遍 
        for(int j=1;j<=n;j++)
        ans=min(ans,f[j][i]);//去最小值 
        if(ans==inf) ans=-1;
        printf("%d\n",ans);//愉快输出 
    }
    return 0;
}

更多优质题目

POJ2411[Mondriaan‘s dream](奶牛吃草题的变形)

POJ2288[Islands and Bridges](较复杂的TSP)

HDU3681[Prison Break](二分答案+状压)

SCOI2005[互不侵犯]

NOIP2016[愤怒的小鸟]

NOIP2017[宝藏]

NOI2015[寿司晚宴]

五、总结

状压dp常常适用于数据规模的某一维或几维非常小，近年来，状压dp越来越常考，几乎年年noip都会出现，下一次考noip的时候，如果你看到这样的数据范围，一定要第一时间想到状态压缩！

状压dp入门

标签：其他   变形   统计   memset   引入   idg   二分答案   space   comment   

原文地址：https://www.cnblogs.com/jvruo/p/10337187.html