标签:text 技术 line 红色 src 傅里叶变换 isp 一次函数 command
笔者学习的是这份博客
内容中可能有很多相同之处,敬请谅解。
现在要计算两个一元\(n\)次多项式\(F(x)\)与\(G(x)\)的乘积,如何计算?
前置知识:多项式的表示方法
一. 系数表示法
对于一个\(n\)次多项式\(F(x)\),它可以被表示成
\[F(x) = a_nx^n+a_{n-1}x^{n-1}+...+a_1x^1+a_0x^0.\]
更加形式化的来说,它可以表示成
\[F(x) = \sum_{i=0}^{n} a_ix^i.\]
举个例子,2次多项式,其中\(a_0=1,a_1=2,a_2=1\)
那么\(F(x)=1x^2+2x+1.\)这样即可通俗的表示出一个\(n\)次多项式。
二. 点值表示法
众所周知,两个点确定一个一次函数,三个点确定一个二次函数。
所以,\(n+1\)个点确定一个一元\(n\)次多项式。
所以我们可以通过\(n+1\)个点来表示它。
那么相乘之后的点值如何计算?
比如说两个2次多项式\(F(x)=x^2+2x+1\)(红色)与\(G(x)=3x^2-4x-2\)(蓝色),它们的图像如图所示:
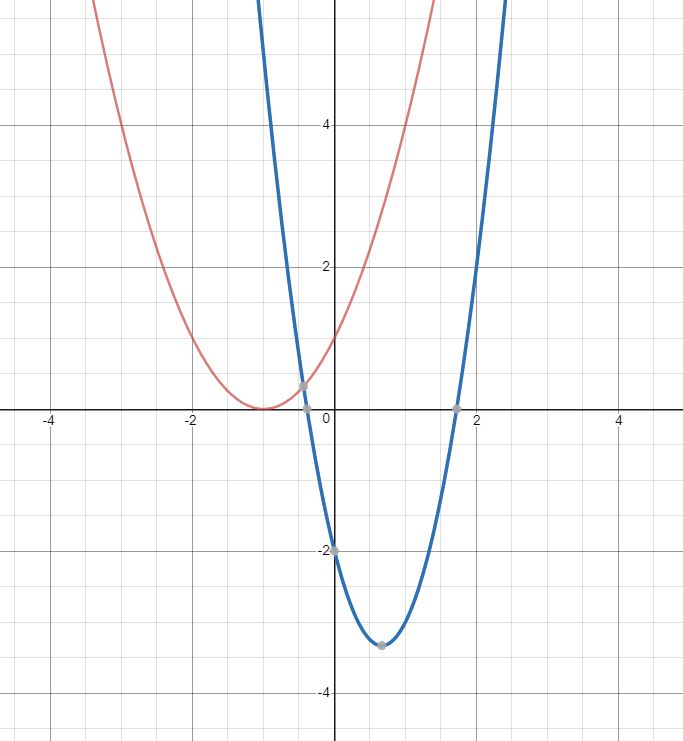
那么观察图中\(x=1\)时的情况。此时\(F(1)=4,G(1)=-3.\)
所以,显然,\(F(1)\times G(1)=-12\).也就是说在\(Z=F*G\)这一多项式内,带入\(1\),得到的结果是\(-12\).
等等,好像有哪里不对。如果说\(Z=F*G\)的话,那么Z的次数应该是\(2n\).
那\(Z\)需要\(2n+1\)个点来确定。但是原来只需要\(n+1\)个点,咋办?
很简单,在原来的多项式里每个都多加\(n\)个点即可。反正多项式已知。
这样就可以用点值来进行操作。也就是说先转成点值,再一乘,再转回来,就是计算流程。
但是好像还是很慢。那么如何优化呢?
复数部分
复数,即形如\(a+bi\)的数,其中\(\sqrt{i}=-1.\) \(a\)称为实部,\(bi\)称为虚部。
或者说:在一个数轴上(只有x轴),我们可以表示出任何实数。
那么,多加一维(y轴),也就是类似于平面直角坐标系一样,我们就可以表示出任意一个复数。
所以我们把这个坐标系叫做复平面,其中x轴称为实轴,y轴称为虚轴。
复数运算
复数相加:实部相加,虚部相加,例如
\[(a+bi)+(c+di)=(a+c)+(b+d)i.\]
复数相减:同理。
\[(a+bi)-(c+di)=(a-c)+(b-d)i.\]
复数相乘:像一次多项式一样相乘。 注意\(i^2=-1\).
\[(a+bi)(c+di)=ac+(ad+bc)i-bd=(ac-bd)+(ad+bc)i.\]
复数相除:
相信大家都学过共轭根式。同样的,复数也有共轭。
即:\(a+bi\)的共轭为\(a-bi\)。
这两个复数卡乘在一起一定是个实数。即
\[(a+bi)(a-bi)=a^2-(bi)^2=a^2+b^2.\]
所以再除的时候,将分子分母同乘分母的共轭,就可以将分母有理化。
即
\[\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{c^2+d^2}=\frac{(ac+bd)}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i.\]
复数逆元:
\[\frac{1}{a+bi}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i.\]
标签:text 技术 line 红色 src 傅里叶变换 isp 一次函数 command
原文地址:https://www.cnblogs.com/LiM-817/p/10340935.html