标签:ret 图片 删掉 9.png 分割线 现在 更新 mes 无向图
强连通分量由美国计算机科学家 Robert Tarjan 提出。
Tarjan
职业:计算机科学家
主要成就:设计了求解的应用领域的许多问题的广泛有效的算法和数据结构等,1986年获得图灵奖.
简介:Robert Tarjan,计算机科学家,以LCA、强连通分量等算法闻名。他拥有丰富的商业工作经验,1985年开始任教于普林斯顿大学。
事实上上述并没有什么用。如果真的想知道就上百度百科吧。
分割线
普及几个强连通分量的定义
强连通: 在一个有向图G里,设两个点 a b 发现,由a有一条路可以走到b,由b又有一条路可以走到a,我们就叫这两个顶点(a,b)强连通
强连通图: 如果 在一个有向图G中,每两个点都强连通,我们就叫这个图为强连通图。
强连通分量:在一个有向图G中,有一个子图,这个子图每2个点都满足强连通,我们就叫这个子图叫做 强连通分量
1.现在是有向图的Tarjan。
先来看个图。
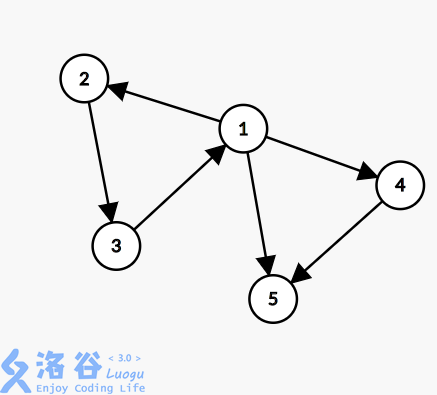
由上述定义知:
子图1,2,3构成一个强连通。
点4独立为一个强连通。
点5也是一个独立的强连通。
相信现在的你已经知道强连通分量究竟是什么了。
然而一个重要的问题产生了:
怎么求它呢???
那么怎么dfs呢?
首先需要三个数组:
1.dfn[Max];(存储时间戳)
2.low[Max];(存储在它之前的最小时间戳)
3.cast[Max];(标记它所在的强连通)

还是刚才的图。
开始时dfn==low;
从1开始(入栈),先搜点2(入栈);
点2再搜点3(入栈),点3搜到了点1,这是点1正在栈中(更新点3的low值;
回溯更新点2的low,再回溯更新点1的low(当然还是原来的low,点1的dfn==low;
此时1搜到4(入栈),点4搜到点5;
点5开始纠结,因为他搜不到别人了,只好老老实实的被使用自己的low;
于是点5的dfn==low成为了一个强连通(出栈);cast[5]=1;
点4也由于点5的low影响不到他,dfn==low,也成为了一个强连通(出栈)。cast[4]=2;
回溯到点1,发现点5已经被访问,而且已经出栈,便不用理他。
此时dfn[1]==low[1]。
开始大批出栈
1出栈,2出栈,3出栈。cast全为3;
那么看一段代码吧:
void tarjan(int x)
{
s.push(x);
ins[x]=1;
inx++;
dfn[x]=low[x]=inx;
for(int i=head[x];i!=-1;i=e[i].next)
{
if(dfn[e[i].to]==0)
{
tarjan(e[i].to);
low[x]=min(low[x],low[e[i].to]);
}
else if(ins[e[i].to]==1)low[x]=min(low[x],dfn[e[i].to]);
}
int v=100000;
if(dfn[x]==low[x])
{
gs++;
while(x!=v)
{
v=s.top();
s.pop();
ins[v]=0;
cast[v]=gs;
}
}
}无向图?
2.无向图的强连通分量。
由于无向图的边可以双向访问,那么只要访问一条边就行了。
看一下代码吧。
void tarjan(int x)
{
int u;
inx++;
dfn[x]=low[x]=inx;
s.push(x);
ins[x]=1;
for(int i=head[x];i!=-1;i=e[i].next)
if(v[i]==0)
{
v[i]=v[i%2==0?i-1:i+1]=1;
u=e[i].to;
if(dfn[u]==0)
{
tarjan(u);
low[x]=min(low[x],low[u]);
}
else if(ins[u]==1)low[x]=min(low[x],dfn[u]);
}
if(dfn[x]==low[x])
{
gs++;
u=Max;
while(u!=x)
{
u=s.top();
s.pop();
ins[u]=0;
cast[u]=gs;
//printf("%d %d\n",u,gs);
}
}
}3.割桥。
定义:在一个无向图中,如果删掉边 x 后图的连通块数量增加,则称点 x 为图的割桥。
我的算法和别的博客不一样。如果有问题可以@我。
连接两个强连通的边是割桥。
貌似不用证明。
代码就同无向图强连通分量了。
4.割点!!!
定义:在一个无向图中,如果删掉点 x 后图的连通块数量增加,则称点 x 为图的割点。
洛谷题目P3388
开始思路为割桥上的点为割点,后来证明的确正确。 不过可惜的是他的逆定理错了(gg了),不过数据很弱以至于得了90分。侥幸
看看下面恶毒地让我90的图吧
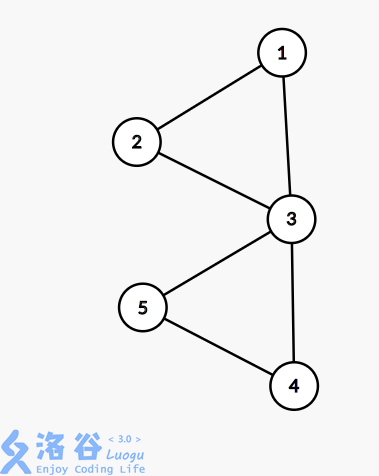
图中无割桥,但点3却是割点,貌似无法解决。
怎样解决???
另一种思路诞生了: 如果u点的子节点为v,v点他能返回的最老祖先比u点年轻或一样(即dfn[u]值<=low[v]),那么如果删去u点,那么v以下的点就会与v以上的点失去联系,就会产生新的连通块(实质是在我的原来思路上多了一个判断
也就是说如果在我们的搜索树上有一个点只有树边与祖先相连,而没有反向边连回祖先节点的话,那么它就是割点。就是没有这样的边 轻微地客串的一个自己的题解,不要举报
代码完整的了
#include<cstdio>
#include<algorithm>
#include<stack>
#include<cstring>
#define Max 1000000+199
using namespace std;
int n,m,dfn[Max]={0},low[Max],cast[Max],ins[Max],inx=0,head[Max],v[Max]={0},cnt=0,gs=0,cd[Max]={0};
stack<int> s;
struct edge
{
int c,to,next;
}e[Max];
void adde(int a,int b)
{
cnt++;
e[cnt].to=b;
e[cnt].c=a;
e[cnt].next=head[a];
head[a]=cnt;
cd[a]++;
}
int ans=0,gd[Max]={0};
void tarjan(int x,int fa)
{
int u,sk=0;
inx++;
dfn[x]=low[x]=inx;
s.push(x);
ins[x]=1;
for(int i=head[x];~i;i=e[i].next)
{
u=e[i].to;
if(dfn[u]==0)
{
tarjan(u,fa);
if(low[u]>=dfn[x]&&x!=fa)gd[x]=1;
v[i]=v[i%2==0?i-1:i+1]=1;
low[x]=min(low[x],low[u]);
if(x==fa)sk++;
}
else if(ins[u]==1&&v[i]==0)v[i]=v[i%2==0?i-1:i+1]=1,low[x]=min(low[x],dfn[u]);
}
if(dfn[x]==low[x])
{
gs++;
u=Max;
while(u!=x)
{
u=s.top();
s.pop();
ins[u]=0;
cast[u]=gs;
//printf("%d %d\n",u,gs);
}
}
if(x==fa&&sk>=2)gd[x]=1;
}
int main()
{
memset(cd,0,sizeof(cd));
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
adde(a,b);
adde(b,a);
//printf("%d",v[i]);
}
for(int i=1;i<=n;i++)
if(dfn[i]==0)tarjan(i,i);
for(int i=1;i<=n;i++)
{
if(gd[i]==1)ans++;
}
printf("%d\n",ans);
for(int i=1;i<=n;i++)
{
if(gd[i]==1)printf("%d ",i);
}
return 0;
}参考文献:
1.https://baike.baidu.com/item/tarjan/8970498?fr=aladdin
2.https://www.luogu.org/blog/zwp/solution-p3388
(真的是我的题解)
标签:ret 图片 删掉 9.png 分割线 现在 更新 mes 无向图
原文地址:https://www.cnblogs.com/zwp2004/p/10346588.html