标签:adt cpp a算法 运算 logs 思想 top 优化 子空间
路径规划是寻路的重要优化思想,在了解路径规划之前必须先了解基本的寻路算法
实际上A寻路算法,对于图也是适用的,实现只要稍微改一下。
大部分讨论A算法使用的是网格点(也就是简单的二维网格),但是这种内存开销往往比较大。
而预先设好路径点,而不是使用网格来当作节点,则可以减少节点数量,顺带也就减少了寻路的运算速度开销。
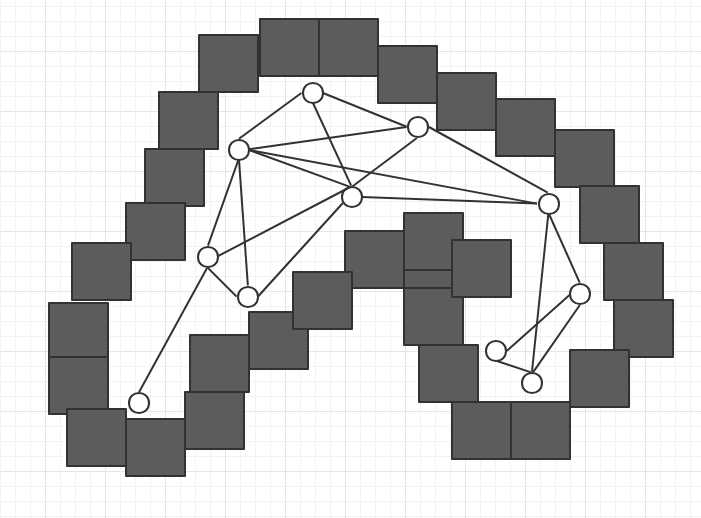
(如图,使用了路径点作为节点)
此外路径点的使用,也能使路径相比网格路径更加平滑。
倘若一个地图过大,开发人员手动预设好路径点+路径连接的工作就比较繁琐,而且很容易有错漏。
这时可以使用洪水填充算法来自动生成路径点,并为它们链接。
算法步骤:
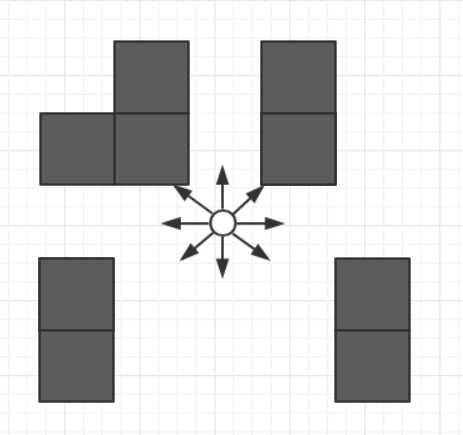
1.以任意一点为起始点,往周围八个方向扩展点(不能通行的位置则不扩展)
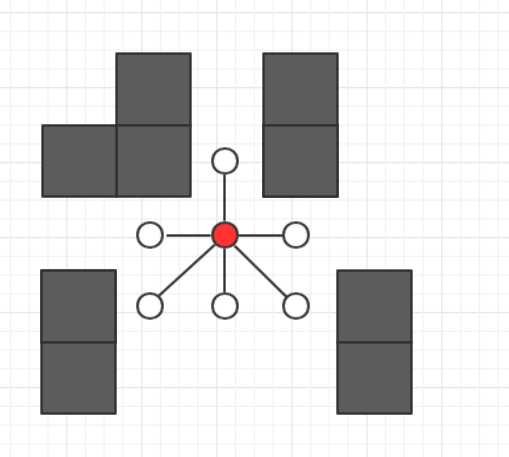
2.已经扩展的点(在图中被标记成红色)不需要再次扩展,而扩展出来新的点继续扩展
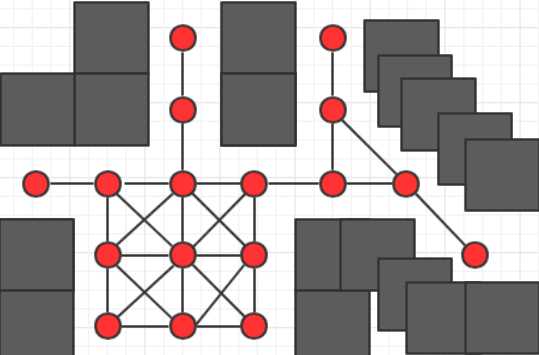
3.直到所有的点都被扩展过,此时能得到一张导航图
//洪水填充法:从一个点开始自动生成导航图
void generateWayPoints(int beginx, int beginy, std::vector<WayPoint>& points) {
//需要探索的点的列表
std::queue<WayPoint*> pointsToExplore;
//生成起点,若受阻,不能生成路径点,则退出
if (!canGeneratePointIn(beginx, beginy))return;
points.emplace_back(WayPoint(beginx, beginy));
//扩展距离
float distance = 2.3f;
//预先写好8个方向的增值
int direction[8][2] = { {1,0}, {0,1}, {0,-1}, {-1,0}, {1,1}, {-1,1}, {-1,-1},{1,-1} };
//以起点开始探索
WayPoint* begin = &points.back();
pointsToExplore.emplace(begin);
//重复探索直到探索点列表为空
while (!pointsToExplore.empty()) {
//先取出一个点开始进行探索
WayPoint* point = pointsToExplore.front();
pointsToExplore.pop();
//往8个方向探索
for (int i = 0; i < 8; ++i) {
//若当前点的目标方向连着点,则无需往这方向扩展
if (point->pointInDirection[i] == nullptr) {
continue;
}
auto x = point->x + direction[i][0] * distance;
auto y = point->y + direction[i][1] * distance;
//如果目标位置受阻,则无需往这方向扩展
if (!canGeneratePointIn(x, y)) {
continue;
}
points.emplace_back(WayPoint(x, y));
auto newPoint = &points.back();
pointsToExplore.emplace(newPoint);
//如果当前点能够无障碍通向目标点,则连接当前点和目标点
if (canWalkTo(point, newPoint)) {
point.connectToPoint(newPoint);
}
}
}
}自动生成的导航图可以调整扩展的距离,从而得到合适的节点和边的数量。
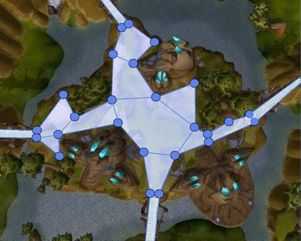
导航网将地图划分成若干个凸多边形,每个凸多边形就是一个节点。
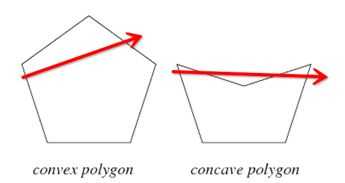
(使用凸多边形,是因为凸多边形边上的一个点走到另外一点,不管怎么走都不会走出这个多边形。而凹多边形可能走的出外面。)
使用导航网更加可以大大减少路径点和搜寻所需的计算量,同时也使路径更加自然。
区域分割有点类似于导航网,但是它属于更高层次的分割。
即完整地图分割成若干个区域,一个区域又可以分割成若干个导航网的凸多边形。
区域分割也不仅可以使用在路径规划上,也可以利用记录区域信息达到很多目的。
例如:AI在感知敌人的时候,可以通过区域分割,过滤掉本区域外的所有敌人,只对本区域的所有敌人作感知测试。
常用的区域分割方法有手动分割区域和使用四叉树(或八叉树)来分割区域。
四叉树索引的基本思想是将地理空间递归划分为不同层次的树结构。
它将已知范围的空间等分成四个相等的子空间,如此递归下去,直至树的层次达到一定深度或者满足某种要求后停止分割。
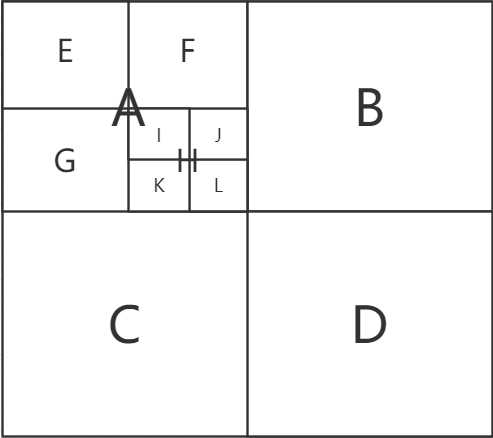
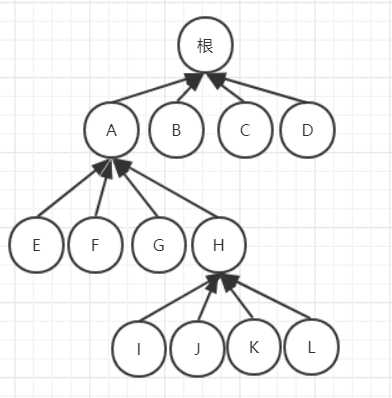
//示例:一个四叉树节点的简单结构
struct QuadtreeNode {
Data data;
QuadtreeNode* children[2][2];
int diliverX; //表示这个区域的划分长度
};//示例:找到x,y位置对应的四叉树节点(共2层)
//通过diliver来将x,y归纳为0或1的值,从而索引到对应的子节点。
int diliver = root.diliver;
int diliverX = x / diliver;
int diliverY = y / diliver;
QuadtreeNode* n1 = root.children[diliverX][diliverY];
//如果归纳为1的值,还需要减去该划分长度,以便进一步划分
x -= diliverX ? diliver : 0;
y -= diliverY ? diliver : 0;
//再执行类似上一操作
diliver = n1.diliver;
diliverX = x / diliver;
diliverY = y / diliver;
QuadtreeNode* n2 = n1.children[x / diliver][y / diliver];
x -= diliverX ? diliver : 0;
y -= diliverY ? diliver : 0;四叉树的结构比较简单,并且当空间数据对象分布比较均匀时,具有比较高的空间数据插入和查询效率(复杂度O(logN))
八叉树类似四叉树,适用于三维空间的分割(一个立方体可被分成8个小立方体)。
主要方式是通过预先计算好的数据,然后运行时使用这些数据减少运算量。
可以根据自己的项目权衡运行速度和内存空间来选择预计算。
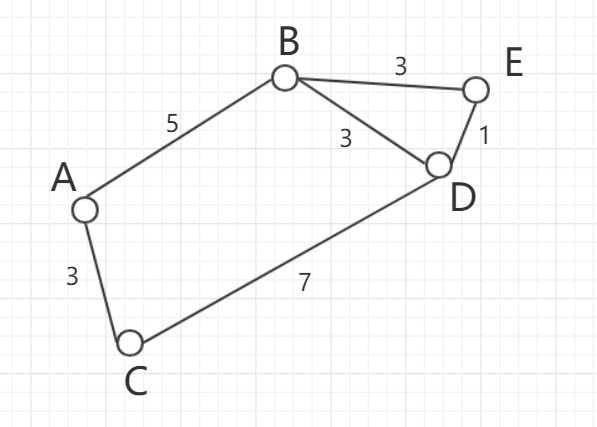
(首先以这副图为示例)
借助预先计算好的路径查询表,可以以O(|v|)的时间复杂度极快完成寻路,但是占用空间为O(|v|2)。
(|v|为顶点数量)
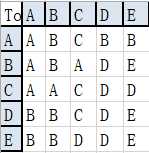
实现:对每个顶点使用Dijkstra算法,求出该顶点到各顶点的路径,再通过对路径回溯得到前一个经过的点。
有时候,游戏AI需要考虑路径的成本来决定行为,
则可以预先计算好路径成本查询表,以O(1)的时间复杂度获取路径成本,但是占用空间为O(|v|2)。
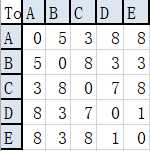
实现:类似路径查询表,只不过记录的是路径成本开销,而不是路径点。
标签:adt cpp a算法 运算 logs 思想 top 优化 子空间
原文地址:https://www.cnblogs.com/KillerAery/p/10283768.html