Canvas动画

时间：2019-02-02 17:10:16 阅读：311 评论：0 收藏：0 [点我收藏+]

标签：fun 本质应用规律三角函数 func speed doc draw

玩Canvas玩了有一个礼拜了平面的东西玩来玩去也就那样所以就开始折腾动画和3D了

什么是动画？

就像思考哲学问题无法回避思维和存在的关系一样制作动画同样无法逃避的问题是动画的原理是什么？

图像序列的变化运动给我们最为直观的感受就是图像仿佛真实的在运动一般由此产生动画效果

我尼玛 Canvas实现物体运动呢？

好了话不多说先上代码

线性运动

物体朝特定方向的运动，运动过程中速度不发生改变

<canvas id="canvas"  width="500" height="500" ></canvas>
    <script>
    //这个脚本中，匀速运动的原理是通过连续改变原点在x轴上的坐标，从而实现匀速运动；
        var canvas = document.getElementById(‘canvas‘);
        var context = canvas.getContext(‘2d‘);

        var ball = new Ball();

        var xspeed = 1;//定义每渲染1帧，图形在x轴移动的距离（移动原点）   

        (function drawFrame(){
            window.requestAnimationFrame(drawFrame,canvas);
            context.clearRect(0,0,canvas.width,canvas.height);

            ball.x += xspeed;
            ball.y = canvas.height/2;

            if(ball.x>canvas.width+ball.radius){
                ball.x = -ball.radius;
            } 

            ball.draw(context);
        })();

    </script>

人类一思考上帝就发笑我一开始的理解为嘲讽人类的自作聪明后来想一下我更加愿意理解为上帝是在对人类不断追求真理这一行为的勉励把

变速运动

变速运动本质上是物体运动过程中速度在变化，也就是加速度的概念

<canvas id="canvas"  width="500" height="500" style="background:#000"></canvas>
   
    <script>

   
        var canvas = document.getElementById(‘canvas‘);
        var context = canvas.getContext(‘2d‘);

        var ball = new Ball();

        var xspeed = 1;//定义每渲染1帧，图形在x轴移动的距离（移动原点）   
        var ax = 0.5;//设置x轴上的每渲染1帧xspeed增加0.05;

        (function drawFrame(){
            window.requestAnimationFrame(drawFrame,canvas);
            context.clearRect(0,0,canvas.width,canvas.height);

            ball.x += xspeed;
            xspeed += ax;
            ball.y = canvas.height/2;
            //ball.y += 1;


            if(ball.x>canvas.width+ball.radius){
                ball.x = -ball.radius;
            } 

            ball.draw(context);
        })();


    </script>

波形运动
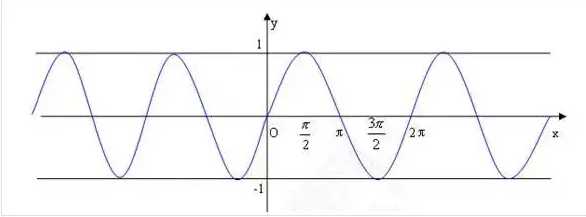
顾名思义像波浪般的运动运动轨迹如同下面的三角函数一般
此时我们不禁想起那夕阳下的奔跑那是我逝去的青春
~~~可是知识已经还给我敬爱的高中老师嘞！

技术图片

//匀速运动
ball.x = xspeed//xspeed = 1一直都是1；

//变速运动
var ax = 0.05;
ball.x += xspeed //xspeed = 1初始值为1；
xspeed += ax//每16ms，xspeed增加0.05；

//波形运动
var angle = 0;//定义每次变化的角度
var swing = 100;//定义振幅；


ball.x +=2;
ball.y  = canvas.height/2 + Math.sin(angle)*swing;
angle += 0.1;

实现代码

<script>

    
        var canvas = document.getElementById(‘canvas‘);
        var context = canvas.getContext(‘2d‘);

        var ball = new Ball();

        var angle = 0;
        var swing = 100;
    

        (function drawFrame(){
            window.requestAnimationFrame(drawFrame,canvas);
            context.clearRect(0,0,canvas.width,canvas.height);

            ball.x += 2;
            ball.y = canvas.height/2+Math.sin(angle)*swing;
            //ball.y += 1;
            angle += 0.1;

            if(ball.x>canvas.width+ball.radius){
                ball.x = -ball.radius;
            } 

            ball.draw(context);
        })();


    </script>

圆形运动

物体的运动规律无非是改变物体在canvas上的坐标值+RAF这个API而产生运动的

x*x+y*y = r*r//这是一原点为圆心 半径为r的圆

//圆的极坐标表达式为
x = rcosθ
y = rsinθ

也就是说给我一个圆的半径和每次旋转的角度 我就可以用x和y的方式描绘圆的路径

二话不说上代码

<script>

    
        var canvas = document.getElementById(‘canvas‘);
        var context = canvas.getContext(‘2d‘);

        var ball = new Ball();

        var angle = 0.1;
        var scope = 100;
    
        (function drawFrame(){
            window.requestAnimationFrame(drawFrame,canvas);
            context.clearRect(0,0,canvas.width,canvas.height);

            ball.x = canvas.width/2+Math.cos(angle)*scope;
            ball.y = canvas.height/2+Math.sin(angle)*scope;
            //ball.y += 1;
            angle += 0.1;

            // if(ball.x>canvas.width+ball.radius){
            //  ball.x = -ball.radius;
            // } 

            ball.draw(context);
        })();


    </script>