标签：开始 ros 变量 产生 问题 避免 节点 今天 上线
二叉树的基本定义结构我们都很熟悉，节点数据加上孩纸指针，左孩子指娘家，右孩子指婆家，我们来看这个例子：
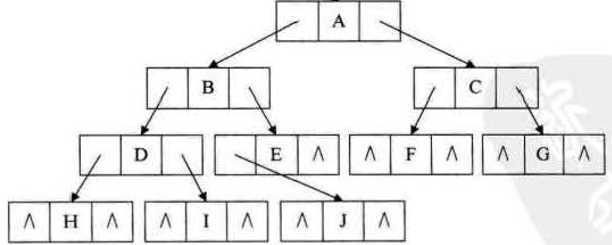
我们会发现，有些孩子并没有地方可以去，例子中的树一共十个结点，十一个空闲指针，由此引出我们对于空闲指针的计算公式：一个有 n 个结点的二叉树有 2n 个指针域，而 n 个结点会产生 n-1 个分支，每个分支对应其指向孩子的指针域，所以空闲指针数： 2n - (n-1) = n+1 ，这么多指针域我们怎样规划能避免这些指针便宜null呢？
大佬们提出了这样一个用途，中序遍历这棵树我们可以得到： HDIBJEAFCG ，很轻松。那么我们可以愉快的知道 I 是 B 的前驱，或者 J 是 B 的后继这样的信息，那是借助了遍历，我们能不能把这些空的指针指向前驱和后继呢，当然阔以。
但是马上有人站出来说，那指向孩子的指针原来就存在了，这后来的野生指针和指向孩子的指针可怎么区分呢，大佬们就决定再加个量来区分指针的类型，如果是指向孩子的就用 0 表示，用作前驱后继的就用 1 表示，使用的时候进行遍历就可以一劳永逸地取得前驱后继的信息，OK，看看结构的定义变成啥样了。
和原来差不多对不对，多了个枚举变量的定义
OK，现在我们的线索二叉树可以算正式出炉辽：
来看一看抽象化结点的结构：
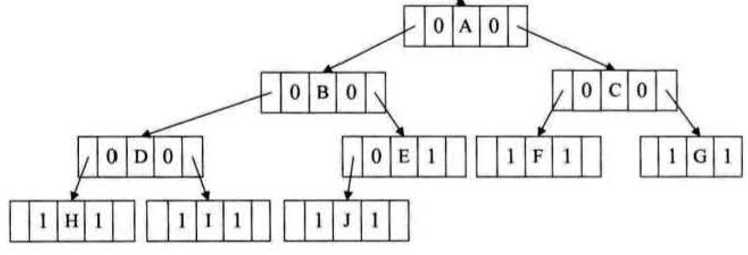改头换面的例子二叉链表
中序线索化遍历的实现
我们来读一下代码，朴素的中序遍历的框架其实还在，中间加粗的是线索化的代码，另外多了 pre 的指针，我们可以发现这个指针永远比我们的主角指针 p 慢一拍，它永远在 p 的前驱结点，每次到了一个结点，我们先判断一哈这个结点有没有左子树，如果没有，就使这个节点的标记值置Thread，表示这个结点被前驱大爷承包了，然后就是让指针 p 的左孩子管 pre 叫干爹， 表示这个结点的前驱就定下了；然后是后继，我们会发现这个和前驱有点不同，这个先看前驱结点的右孩子是否为空，即 如果 pre -> rchild 为空，就把这个引到 p 指针，我们说 p 指针走的快一步，所以这就找到了后继，顺理成章 pre->rtag = Thread，pre -> rchild = p; 完美！ 这两步表示一轮线索化的一个轮回，弄完这些让 pre 再向前走一步，就是 pre = p，剩下的和中序遍历没什么区别
我们给这个二叉链表加上一个头指针，并且让头结点的左孩子指向树根节点，让中序的第一个节点指回头结点的左孩子指针，用头结点的右指针指向中序遍历的最后一个结点，并且把这个指针指回头结点的右指针，形成双向的指针循环，这样的好处就在于既可以从第一个结点开始沿中序的后继向后遍历，也可以利用从头开始前序遍历（例子及表述来自《大话数据结构》）
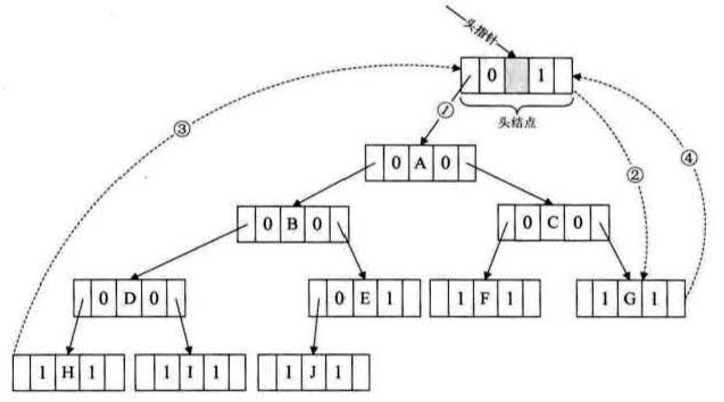
附上带头结点的线索二叉树中序遍历：
首先定义指向根的头结点 p，我们先看外层这个最大的循环，这个循环条件为 p != T ，这个条件首先排除了空树的遍历，其次按照刚才对带头节点二叉线索表的分析，最后的 p 指针会在穷途末路时等于 T ，这相当于 p 指向头结点，这时 p = T ，故如果不加 p != T ，则会无限循环下去。进入循环，首先是判定p -> ltag 等于Link，内容是指向左子树，那么这一个循环表示从根开始直到没有左子树的末端，路径是A →B→D→H，然后打印H，目前 p 的右指针是指向直接后继D的，所以下面一个进入第二个while，打印出D，D的右边是孩子指针，第十五行指向I，然后重复整个过程，相当于从小树到大树以链表搜索的形势进行完整的中序遍历，完整顺序参照下图
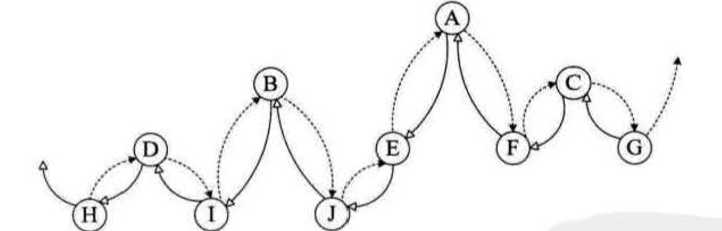
好的，我们今天的线索二叉树就到这里辽，最后附上一段我偷来的话：
标签：开始 ros 变量 产生 问题 避免 节点 今天 上线
原文地址：https://www.cnblogs.com/yx1999/p/10352285.html
