标签:system method eth sqrt void style 思路 span %x
题目:
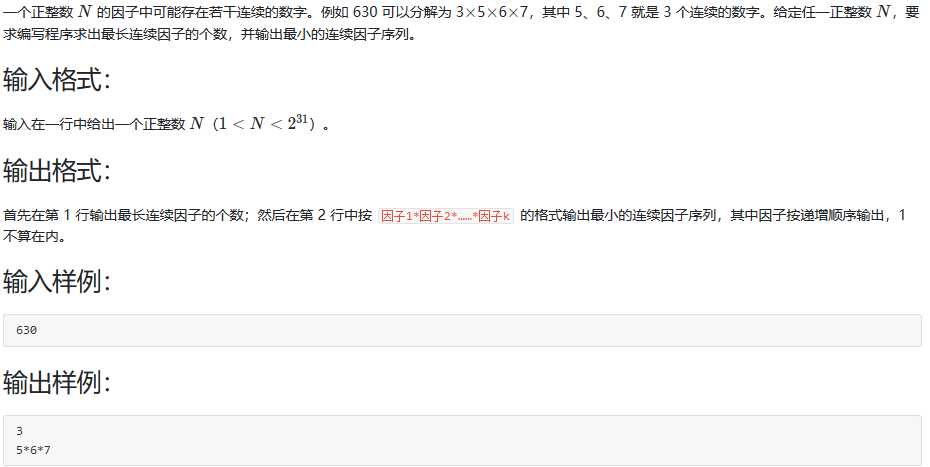
思路:连续因子的范围一定是从1到sqrt(N),因为如果有一个数超过sqrt(N)了,那么无论它与前一个数还是后一个数相乘都会大于N。所以在1到sqrt(N)中暴力找出能被N整除的连续相乘的数串即可。如果N是质数,要另作考虑,输出的结果就是1和N。
上代码:
import java.util.*; public class Main { public static void main(String[] args) { // TODO Auto-generated method stub Scanner sc=new Scanner(System.in); int n=sc.nextInt(); int maxn=(int) Math.sqrt(n); int i,j,len = 0,first=0; for(i=2;i<=maxn;i++) { int x=1;//因数 for(j=i;j<=maxn;j++) { x *= j; if(n%x!=0) break; } if(j-i>len){ len=j-i; first=i; } } if(len==0) { System.out.println("1"); System.out.print(n); } else{ System.out.println(len); for(i=0;i<len-1;i++) { System.out.print(first+i+"*"); } System.out.print(first+len-1); } } }
疑问:虽然这么做能AC,但是我不太知道为什么要写n%x!=0,难道判断他是否能被整除不应该是n%x==0吗?还有为什么len是 j-i 而不是 j-i+1?想了半天还是不明白。。。
标签:system method eth sqrt void style 思路 span %x
原文地址:https://www.cnblogs.com/littleLittleTiger/p/10355046.html