标签:信息 void 总数 stream 位置 简单图 push iter mic
参考书籍: 算法(第4版).[美]Robert Sedgewick
必须要满足以下两点:
逻辑结构分为两部分:
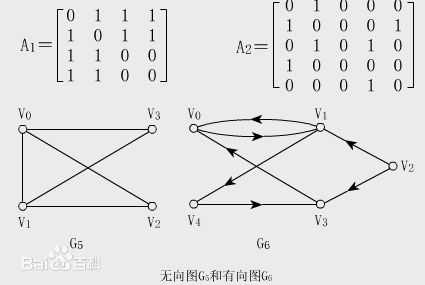
Vexs[ ](存储顶点)用一个一维数组存放图中所有顶点数据;
Edges[ ][ ](邻接矩阵)集合,用一个二维数组存放顶点间关系(可以是权重,也可以是0,1)的数据,这个二维数组称为邻接矩阵。
typedef struct AdjMatrix{ int *Vexs; int **Edges; int vexnum, edgenum; // 顶点数,边数 }*Graph;
规定输入:
#include <stdio.h> #include <string.h> #include <malloc.h> typedef struct AdjMatrix{ int *Vexs; int **Edges; int vexnum, edgenum; // 顶点数,边数 }*Graph; //vn:vexnum;en:edgenum Graph init(int vn,int en) { Graph g = (Graph)malloc(sizeof(AdjMatrix)); g->vexnum = vn; g->edgenum = en; g->Vexs = (int *)malloc(sizeof(int)*vn); for (int i = 0; i < vn; i++) { scanf("%d",&g->Vexs[i]); } g->Edges = (int **)malloc(sizeof(int*)*vn); for (int i = 0; i < vn; i++) { g->Edges[i] = (int *)malloc(sizeof(int)*vn); memset(g->Edges[i], 0, sizeof(int)*vn); } for (int i = 0; i < en; i++) { int column,row; scanf("%d%d", &row,&column); g->Edges[row - 1][column - 1] = 1; //有向图把下面一行注释掉 g->Edges[column - 1][row - 1] = 1; } return g; } void traverse(Graph g) { for (int i = 0; i < g->vexnum; i++) { for (int j = 0; j < g->vexnum; j++) { printf("%4d ", g->Edges[i][j]); } printf("\n"); } } int main() { int vn, en;//顶点个数、边个数 scanf("%d%d",&vn,&en); Graph g = init(vn, en); traverse(g); return 0; }
写到这也能看出来了邻接矩阵可以快速判断两个顶点之间是否存在边、添加边或者删除边(通过索引 O(1))。
但是缺点也很致命存储稀疏矩阵时,十分较浪费空间,这显然不满足第一个条件。也就引申出了邻接表。
邻接表是一种顺序分配和链式分配相结合的存储结构。可以说是简化版的十字链表。
N个顶点,对应N个表头节点,如果某个表头结点,所对应的顶点存在相邻顶点,则把相邻顶点依次(按顶点顺序)存放于表头结点所指向的单向链表中。
规定输入:
完整代码(不带权重):
#include <iostream> #include <map> #include <list> #include <queue> #include <set> using namespace std; class node { public: int data; node* next; node(int d) { data = d; next = NULL; } }; class AdjList { public: map<int, node*> listhead; int vexnum, edgenum; // 顶点数,边数 AdjList(int vn, int en) { vexnum = vn; edgenum = en; for (int i = 0; i < en; i++) { int from, to; cin >> from >> to; if (!listhead[from]) { listhead[from] = new node(from); } if (!listhead[to]) { listhead[to] = new node(to); } node *s = new node(to); s->next = listhead[from]->next; listhead[from]->next = s; //有向图就是把下面三行删掉 s = new node(from); s->next = listhead[to]->next; listhead[to]->next = s; } } }; typedef AdjList* Graph; void print(Graph g) { map<int, node *>::iterator it = g->listhead.begin(); while (it != g->listhead.end()) { node *p = it->second->next; cout << it->second->data << " :"; while (p) { cout << p->data << " "; p = p->next; } cout << endl; it++; } }
邻接表和邻接矩阵这两种方式是最常见的,但是邻接表还是会有部分空间浪费,因为每条链表里用的node是独立的。
看了严蔚敏教授的数据结构教材书上的数据结构,我认为真的太繁琐了,
#define N 200 typedef struct ArcNode { int adjvex;//该弧指向的顶点的位置 ArcNode *nextarc;//指向下一条弧的指针 int *info; //该弧的相关信息 }; typedef struct { VertexType data;//顶点信息 ArcNode *firstarc; //指向第一条依附该顶点的弧的指针 } VNode,AdjList[N]; typedef struct ALGraph { AdjList vertices; int vexnum,arcnum;//弧的当前顶点数和弧数 int kind;//图的种类 };
自己写了一个,借助map,直接可以用下标来找表头了。
class node { public: int data;//该节点的数据 vector<node *>next; vector<int>weight; }; class AdjList { public: map<int, node *>Nodes; }
广度优先搜索算法(Breadth-First-Search,缩写为 BFS),是一种利用队列实现的搜索算法。其搜索过程和 “水滴落下产生波纹” 类似。
因为每条链表里相同data的节点时独立存在的,BFS、DFS要判断当前节点是否输出过,就要放到set里,如果存节点的话,那肯定得用set<node *>;因为set<node>的话,set里存的就不是指针了,占空间更多。但是存指针问题就来了,相同data的节点是独立的,那么set里就只能添加node->data
对于遍历而言,没有有向图、无向图之分。这里不考虑非连通图。(非连通,再加一个大循环,很好实现)
void BFS() { queue<node *>queue; set<node*>set; node *n = Nodes.begin()->second; queue.push(n); set.insert(n); cout << n->data << " "; while (!queue.empty()) { node *p = queue.front(); queue.pop(); for (int i = 0; i < p->next.size(); i++) { if (set.find(p->next[i]) == set.end()) { cout << p->next[i]->data << ‘ ‘; set.insert(p->next[i]); queue.push(p->next[i]); } } } }
深度优先搜索算法(Depth-First-Search,缩写为 DFS),是一种利用递归(栈)实现的搜索算法。其过程像 “不撞南墙不回头” 类似。
void DFS() { stack<node *>stack; set<node *>set; node *n = Nodes.begin()->second; stack.push(n); set.insert(n); while (!stack.empty()) { node *p = stack.top(); stack.pop(); cout << p->data << ‘ ‘; for (int i = 0; i < p->next.size(); i++) { if (set.find(p->next[i]) == set.end()) { set.insert(p->next[i]); stack.push(p->next[i]); } } } }
留档一下:邻接表的BFS、DFS

void BFS(Graph g) { queue<node *>q; set<int>s; map<int, node*>::iterator it = g->listhead.begin(); node *n = it->second; q.push(n); s.insert(n->data); cout << n->data << " "; while (!q.empty()) { node *p = q.front(); q.pop(); while (p) { if (s.find(p->data) == s.end()) { cout << p->data << " "; s.insert(p->data); q.push(g->listhead[p->data]); } p = p->next; } } } void DFS(Graph g) { stack<node *>stack; set<int>set; map<int, node*>::iterator it = g->listhead.begin(); node *p = it->second; stack.push(p); set.insert(p->data); while (!stack.empty()) { p = stack.top(); stack.pop(); cout << p->data << " "; while (p->next) { p = p->next; if (set.find(p->data) == set.end()) { stack.push(g->listhead[p->data]); set.insert(p->data); } } } }
第三种实现的完整代码:

class node { public: int data;//该节点的数据 vector<node *>next; vector<int>weight; node(int data) { this->data = data; } }; class AdjList { public: map<int, node *>Nodes; AdjList(int en) { while (en--) { int from, to, weight; cin >> from >> to >> weight; if (!Nodes[from]) { Nodes[from] = new node(from); } if (!Nodes[to]) { Nodes[to] = new node(to); } node *p = Nodes[from], *q = Nodes[to]; p->next.push_back(q); p->weight.push_back(weight); q->next.push_back(p); q->weight.push_back(weight); } } /*void BFS() { map<int, node* >::iterator it = Nodes.begin(); node *n = it->second; queue<node *>q; set<node *>s; q.push(n); s.insert(n); while (!q.empty()) { node *n = q.front(); q.pop(); cout << n->data << " "; for (int i = 0; i < n->next.size(); i++) { node *p = n->next[i]; if (s.find(p) == s.end()) { s.insert(p); q.push(p); } } } }*/ void BFS() { queue<node *>queue; set<node*>set; node *n = Nodes.begin()->second; queue.push(n); set.insert(n); cout << n->data << " "; while (!queue.empty()) { node *p = queue.front(); queue.pop(); for (int i = 0; i < p->next.size(); i++) { if (set.find(p->next[i]) == set.end()) { cout << p->next[i]->data << ‘ ‘; set.insert(p->next[i]); queue.push(p->next[i]); } } } } void DFS() { stack<node *>stack; set<node *>set; node *n = Nodes.begin()->second; stack.push(n); set.insert(n); while (!stack.empty()) { node *p = stack.top(); stack.pop(); cout << p->data << ‘ ‘; for (int i = 0; i < p->next.size(); i++) { if (set.find(p->next[i]) == set.end()) { set.insert(p->next[i]); stack.push(p->next[i]); } } } } }; typedef AdjList *Graph;
写了几题BFS、DFS的练习题,才发现,DFS BFS是思想,基本上是碰不到能完全套模板的题目。
---------这---------是---------一---------条---------分---------割---------线---------
标签:信息 void 总数 stream 位置 简单图 push iter mic
原文地址:https://www.cnblogs.com/czc1999/p/10353235.html