最长公共子序列 与 最长公共连续子串

//最长公共子序列(个数)
#include<iostream>
using namespace std;
int c[100][100]={0};
int len1,len2;
int  gcd(string a,string b){
    len1=a.length(); 
    len2=b.length();
    int tmp=-1;
    for(int i=0;i<len1;i++)
    {
        for(int j=0;j<len2;j++){
            if(a[i]==a[j]) c[i][j]=c[i-1][j-1]+1;
            else c[i][j]=max(c[i-1][j],c[i][j-1]);
            if(tmp<c[i][j]) tmp=c[i][j];
        }
    }
    return tmp;
}

int main()
{
    string a,b;
    while(cin>>a>>b){
    cout<<gcd(a,b);    
    }
} 

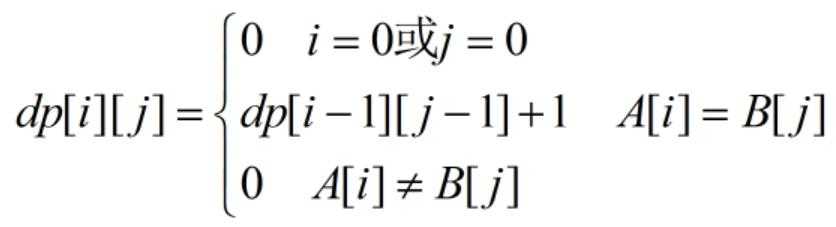
#include<iostream>
#include<string.h>
using namespace std;
 
void print_substring(string str, int end, int length)
{
    int start = end - length + 1;
    for(int k=start;k<=end;k++)
        cout << str[k];
    cout << endl;
}
 
int main()
{
    string A,B;
    cin >> A >> B;
    int x = A.length();
    int y = B.length();
    A = " " + A;//特殊处理一下，便于编程 
    B = " " + B;
    
    //回忆一下dp[][]的含义？ 
    int **dp = new int* [x+1];
    int i,j;
    for(i=0;i<=x;i++)
    {
        dp[i] = new int[y+1];
        for(j=0;j<=y;j++)
            dp[i][j] = 0;
    }
    
    
    //下面计算dp[i][j]的值并记录最大值 
    int max_length = 0;
    for(i=1;i<=x;i++)
        for(j=1;j<=y;j++)
            if(A[i]==B[j])
            {
                dp[i][j] = dp[i-1][j-1] + 1;
                if(dp[i][j]>max_length)
                    max_length = dp[i][j];
            }
            else
                dp[i][j] = 0;
 
    
    //LCS的长度已经知道了，下面是根据这个最大长度和dp[][]的值，
    //找到对应的 LCS具体子串， 注意：可能有多个 
    int const arr_length = (x>y?x:y) + 1;
    int end_A[arr_length];    //记录LCS在字符串A中结束的位置 
    int num_max_length = 0;    //记录LCS的个数 
    
    for(i=1;i<=x;i++)
        for(j=1;j<=y;j++)
            if(dp[i][j] == max_length)
                end_A[num_max_length++] = i;
    
    cout << "the length of LCS(substring) is : " << max_length  << endl << " nums: " << num_max_length << endl << "they are (it is): " << endl;
    for(int k=0;k<num_max_length;k++)    //输出每个具体的子串 
        print_substring(A, end_A[k], max_length);
    
    return 0;
}