【模版】线性筛（素数,欧拉函数,莫比乌斯函数）

标签：int   code   efi   ++   ima   http   比较   for   jpg   

线性筛:

线性筛是一种比较实用的筛法，它与数论中的（完全）积性函数密切相关：

（完全）积性函数的定义：对于两个整数 \(x_1\) 和 \(x_2\) ，若有函数\(f(x)\)满足：\(f(x_1x_2)=f(x_1)f(x_2)\)，我们称\(f(x)\)为完全积性函数；特殊的：若 \(x_1\) 和 \(x_2\) 一定为两个互质的正整数，我们称\(f(x)\)为积性函数！

而线性筛就是利用了这一性质，将\(f(x)\)用且只用\(x\)最小的那个质因子利用\(f(x_1x_2)=f(x_1)f(x_2)\)将它算出来，这样就能避免许多重复情况。

然后讲一下我们最基础的筛素数吧：

线性筛素数:

虽然素数不是什么积性函数，但它和我们的思路一致：将某个合数用且只用它最小的质因子筛掉。

#define rg register int
vector<int> prime;
bool pr[100005];

inline void _prime(int n){//求n以内的素数
    for(rg i=2;i<=n;++i) pr[i]=1;
    for(rg i=2;i<=n;++i){
        if(pr[i])prime.push_back(i);//没筛掉说明它是素数
    for(rg j=0;j<prime.size();++j){
            if(i*prime[j]>n)break;//剪枝
            pr[i*prime[j]]=0;
            if(!(i%prime[j]))break;//保证用且只用最小的质因子把它筛去
        }
    }return ;
}

线性筛欧拉函数\((\phi)\)：

欧拉函数($\phi \()定义：\)\phi (x)\(表示比\)x\(小的与\)x\(互质的数的个数（\)\phi(1)=1$）

性质1 ：对于质数\(x\)显然有：\(\phi(x)=x-1\)

性质 2：对于质数\(x\)显然有：\(\phi(2*x)=\phi(x)\)

性质 3：与费马小定理：\(a^{?(m)}≡1(mod\) \(m)\)

性质 4：对于质数\(p\)：若 \(i\) \(mod\) $ p$ \(==\) \(0\) 则有：\(\phi(i*p)=\phi(i)*p\)

性质 5：对于质数\(p\)：若 \(i\) \(mod\) $ p$ \(!=\) \(0\) 则有：\(\phi(i*p)=\phi(i)*(p-1)\)

利用性质4和性质5，我们可以将欧拉函数和质数一起筛：

#define rg register int
vector<int> prime;
int phi[100005];//phi数组可以用来判断负数的

inline void _phi(int n){
    phi[1]=1;
    for(rg i=2;i<=n;++i){
        if(!phi[i])phi[i]=i-1,prime.push_back(i);
        for(rg j=0;j<prime.size();++j){
            if(i*prime[j]>n)break;
            if(!(i%prime[j])){
                phi[i*prime[j]]=phi[i]*prime[j];//性质4
                break;//这个if用得真的很妙的！
            }else phi[i*prime[j]]=phi[i]*phi[prime[j]];//性质5
        }
    }return ;
}

线性筛莫比乌斯函数\((\mu)\)：

莫比乌斯函数通俗定义：

1）莫比乌斯函数\(μ(n)\)的定义域是N

2）\(μ(1)=1\)

3）当n存在平方因子时，\(μ(n)=0\)

4）当n是素数或奇数个不同素数之积时，\(μ(n)=-1\)

5）当n是偶数个不同素数之积时，\(μ(n)=1\)

即：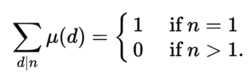

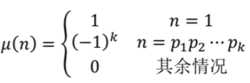
利用性质4和性质5，我们可以将莫比乌斯函数和质数一起筛：

#define rg register int
vector<int> prime;
int mu[100005];
bool use[100005];

inline void _mu(int n){
    mu[1]=1;
    for(rg i=2;i<=n;++i){
        if(!use[i])mu[i]=-1,prime.push_back(i);
        for(rg j=0;j<prime.size();++j){
            if(i*prime[j]>n)break;
            use[i*prime[j]]=1;
            if(!(i%prime[j])) break;
            else mu[i*prime[j]]=-mu[i];
        }
    }return ;
}

【模版】线性筛（素数,欧拉函数,莫比乌斯函数）

标签：int   code   efi   ++   ima   http   比较   for   jpg   

原文地址：https://www.cnblogs.com/812-xiao-wen/p/10357600.html