求平面内最近点对

标签：mamicode   display   两种   etc   include   排序   技术   mat   lock   

 　　传送门

分治

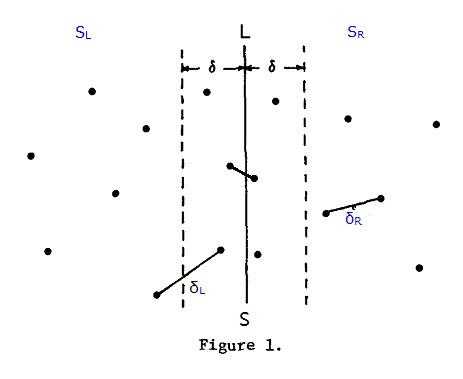
　　如图 在平面内作一条竖直线把平面分为左右两部分 使得点尽量均匀地分布在竖直线两侧

　　那么最近点对只有三种情况（如图）：

　　　　1.两点都在左边 2.两点都在右边 3.一点在左一点在右

　　1,2两种情况其实和现在这种情况是一样的 递归求解即可

　　我们要解决的是中间的情况

　　令左边求出的最近点对距离为a，右边求出的为b

　　d=min(a,b)

　　然后从竖直线往左、右扩展d 包括在内的点再按y排序

　　用这些点的距离来更新ans即可　　

CODE：

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<algorithm>
 5 #define R register
 6 #define go(i,a,b) for(R int i=a;i<=b;i++)
 7 #define ll long long
 8 #define db double
 9 #define M 200000+1
10 #define inf 10e64
11 using namespace std;
12 int read()
13 {
14     int x=0,y=1;;char c=getchar();
15     while(c<‘0‘||c>‘9‘) {if(c==‘-‘) y=-1;c=getchar();}
16     while(c>=‘0‘&&c<=‘9‘) {x=(x<<3)+(x<<1)+c-‘0‘;c=getchar();}  
17     return x*y;
18 }
19 struct node{int x,y;}a[M],b[M];
20 int n;
21 bool cmp1(node u,node v){return u.x==v.x?u.y<v.y:u.x<v.x;}
22 bool cmp2(node u,node v){return u.y<v.y;}
23 ll sq(int x){return (ll)x*x;}
24 ll dis(int u,int v){return sq(a[u].x-a[v].x)+sq(a[u].y-a[v].y);}
25 ll sol(int l,int r)
26 {
27     if(l>=r) return inf;
28     if(r==l+1) return dis(l,r);
29     int mid=(l+r)>>1,midx=a[mid].x,ct=0;
30     ll d=min(sol(l,mid),sol(mid+1,r));
31     go(i,l,r) if(sq(a[i].x-midx)<=d) b[++ct]=a[i];
32     sort(b+1,b+ct+1,cmp2);
33     go(i,1,ct)
34         go(j,i+1,ct)
35     {
36         if(sq(b[i].y-b[j].y)>d) break;
37         d=min(d,sq(b[i].x-b[j].x)+sq(b[i].y-b[j].y));
38     }
39     return d;
40 }
41 int main()
42 {
43     //freopen("1.in","r",stdin);
44     //freopen("1.out","w",stdout);
45     n=read();
46     go(i,1,n) a[i].x=read(),a[i].y=read();
47     sort(a+1,a+n+1,cmp1);
48     printf("%.4lf",(db)sqrt(sol(1,n)));
49     return 0;
50 }

View Code

 

求平面内最近点对

标签：mamicode   display   两种   etc   include   排序   技术   mat   lock   

原文地址：https://www.cnblogs.com/forward777/p/10360073.html