标签:let clu amp alt ntb idt print 归一化 count()
在OpenCV中,实现直方图均衡化比较简单,调用equalizeHist函数即可。具体代码如下:
#include <iostream>
#include <opencv2\opencv.hpp>
using namespace std;
using namespace cv;
int main()
{
Mat srcImage;
srcImage = imread("D:\\Data\\imgDemo\\lena512color.bmp", IMREAD_GRAYSCALE);
imshow("原图像", srcImage);
Mat dstImage;
equalizeHist(srcImage, dstImage);
imshow("均衡后", dstImage);
waitKey();
return 0;
}注意equalizeHist函数处理的是8位单波段的mat。运行结果如下所示,可以发现经过直方图均衡化之后,图像的对比度增强了很多。
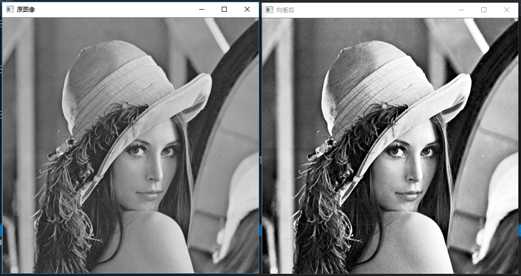
直方图均衡化的基本思想是把原始图的直方图尽可能的均匀分布,其数学原理与数学中的概率论相关。注意,我这里很多论述牺牲了数学的严密性来加强可理解性,毕竟作者只是个应用者和使用者。
具体到一张图像上来说,可以把图像的灰度(像素值)ri看作是随机变量,则可以知道图像灰度的概率为:
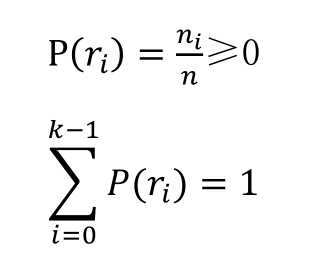
对应的,对于一个连续型的随机变量x,如果存在函数f(x)也满足上面两个条件:
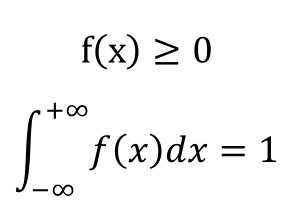
则这个函数就是概率密度函数。
离散随机变量的概率有具体的公式让你理解,那么连续随机变量的概率密度函数具体的公式是怎么样的呢?这个概念其实需要下面要介绍的概率分布函数来理解。
概率分布函数就是是概率密度函数的变上限积分:
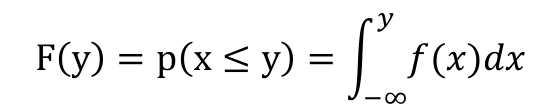
通俗来讲,概率分布函数就是所有小于当前随机变量的概率累加。所以,概率分布函数也被叫做累积概率函数。
知道概率分布函数,引用下网上相关论述[1]就能更好的理解概率密度函数了:

直方图均衡化变换就是一种灰度级非线性变换,设r和s分别表示变换前和变换后的灰度,且r和s都进行了归一化的处理。则直方图均衡化变换的公式为:
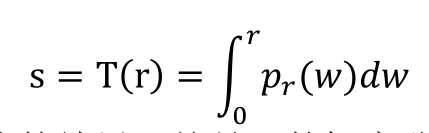
即归一化后,直方图均衡化的结果s就是r的概率分布函数。
根据概率论随机变量的函数的分布的相关知识,有s的概率密度函数为
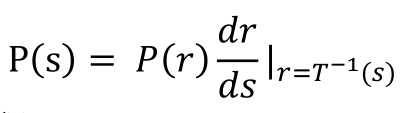
以下[2]具体论述了其应用过程:


继续推导,有:
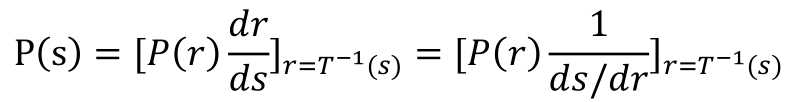
其中s为r的概率分布函数,则:
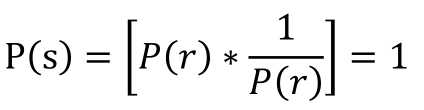
变换后变量s的概率密度为常数,说明其概率密度为均匀分布的。
根据第二节的论述,就知道直方图均衡化的具体操作了,可以分成以下几步:
其具体代码实现如下,我这里是采用 GDAL 来读取影像的,因为我想直接操作读
取的内存 buf,这样更底层一些。如果你不会使用 GDAL 也没有关系,你只需要
知道 GDAL 读取的是按照 RGBRGBRGB…排序的内存 buf。
#include <iostream>
#include <algorithm>
#include <gdal_priv.h>
using namespace std;
//直方图均衡化
void GetHistAvgLut(GUIntBig* anHistogram, int HistNum, vector<uint8_t > &lut)
{
//统计像素总的个数
size_t sum = 0;
for (int ci = 0; ci < HistNum; ci++)
{
sum = sum + anHistogram[ci];
}
//
vector<double> funProbability(HistNum, 0.0); //概率密度函数
vector<double> funProbabilityDistribution(HistNum, 0.0); //概率分布函数
//计算概率分布函数
double dsum = (double)sum;
double accumulation = 0;
for (int ci = 0; ci < HistNum; ci++)
{
funProbability[ci] = anHistogram[ci] / dsum;
accumulation = accumulation + funProbability[ci];
funProbabilityDistribution[ci] = accumulation;
}
//归一化的值扩展为0~255的像素值,存到颜色映射表
lut.resize(HistNum, 0);
for (int ci = 0; ci < HistNum; ci++)
{
double value = std::min<double>(std::max<double>(255 * funProbabilityDistribution[ci], 0), 255);
lut[ci] = (unsigned char)value;
}
}
//计算16位的颜色映射表
bool CalImgLut(GDALDataset* img, vector<vector<uint8_t>>& lut)
{
int bandNum = img->GetRasterCount(); //波段数
lut.resize(bandNum);
//
for (int ib = 0; ib < bandNum; ib++)
{
//计算该通道的直方图
int HistNum = 256;
GUIntBig* anHistogram = new GUIntBig[HistNum];
int bApproxOK = FALSE;
img->GetRasterBand(ib + 1)->GetHistogram(-0.5, 255.5, HistNum, anHistogram, TRUE, bApproxOK, NULL, NULL);
//直方图均衡化
GetHistAvgLut(anHistogram, HistNum, lut[ib]);
//
delete[] anHistogram;
anHistogram = nullptr;
}
return true;
}
int main()
{
//
GDALAllRegister(); //GDAL所有操作都需要先注册格式
CPLSetConfigOption("GDAL_FILENAME_IS_UTF8", "NO"); //支持中文路径
//读取
const char* imgPath = "D:\\Data\\imgDemo\\lena512color.bmp";
GDALDataset* img = (GDALDataset *)GDALOpen(imgPath, GA_ReadOnly);
if (!img)
{
cout << "Can‘t Open Image!" << endl;
return 1;
}
//
int imgWidth = img->GetRasterXSize(); //图像宽度
int imgHeight = img->GetRasterYSize(); //图像高度
int bandNum = img->GetRasterCount(); //波段数
int depth = GDALGetDataTypeSize(img->GetRasterBand(1)->GetRasterDataType()) / 8; //图像深度
//创建颜色映射表
vector<vector<uint8_t>> lut;
CalImgLut(img, lut);
//创建
GDALDriver *pDriver = GetGDALDriverManager()->GetDriverByName("BMP"); //图像驱动
char** ppszOptions = NULL;
const char* dstPath = "D:\\Data\\imgDemo\\dst.bmp";
int bufWidth = imgWidth;
int bufHeight = imgHeight;
GDALDataset* dst = pDriver->Create(dstPath, bufWidth, bufHeight, bandNum, GDT_Byte, ppszOptions);
if (!dst)
{
printf("Can‘t Write Image!");
return false;
}
//读取buf
size_t imgBufNum = (size_t)bufWidth * bufHeight * bandNum * depth;
GByte *imgBuf = new GByte[imgBufNum];
img->RasterIO(GF_Read, 0, 0, bufWidth, bufHeight, imgBuf, bufWidth, bufHeight,
GDT_Byte, bandNum, nullptr, bandNum*depth, bufWidth*bandNum*depth, depth);
//迭代通过颜色映射表替换值
for (int yi = 0; yi < bufHeight; yi++)
{
for (int xi = 0; xi < bufWidth; xi++)
{
for (int bi = 0; bi < bandNum; bi++)
{
size_t m = (size_t)bufWidth * bandNum * yi + bandNum * xi + bi;
imgBuf[m] = lut[bi][imgBuf[m]];
}
}
}
//写入
dst->RasterIO(GF_Write, 0, 0, bufWidth, bufHeight, imgBuf, bufWidth, bufHeight,
GDT_Byte, bandNum, nullptr, bandNum*depth, bufWidth*bandNum*depth, depth);
//释放
delete[] imgBuf;
imgBuf = nullptr;
GDALClose(dst);
dst = nullptr;
GDALClose(img);
img = nullptr;
return 0;
}可以看到我这里统计了0到255的直方图之后,归一化计算每个像素的分布概率,再还原成0到255的值并预先生成了一个颜色映射表,最后直接通过这个颜色映射表进行灰度变换。这是图像处理的一种加速办法。最终得到的结果对比:
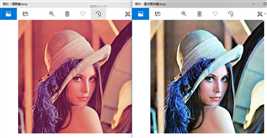
其直方图对比:
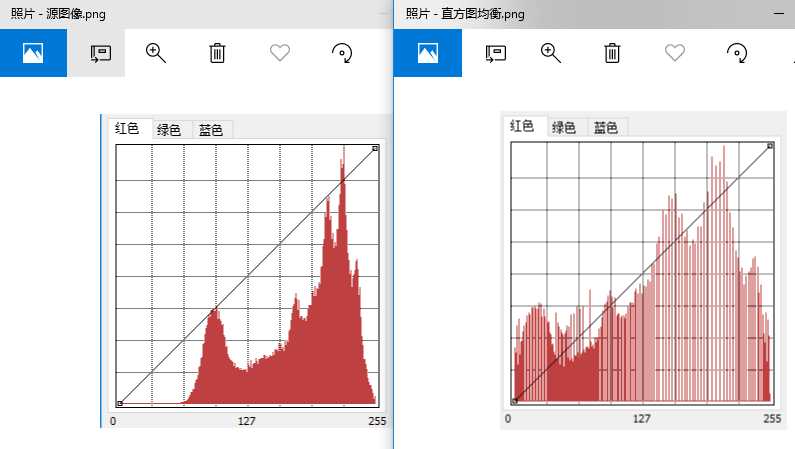
[1] 应该如何理解概率分布函数和概率密度函数
[2] 直方图均衡化的数学原理
[3] 理解概率密度函数
[4] 直方图均衡化的数学原理
[5] 直方图均衡化(Histogram equalization)与直方图规定化
标签:let clu amp alt ntb idt print 归一化 count()
原文地址:https://www.cnblogs.com/charlee44/p/10360616.html