$Matrix-Tree$定理-题目

标签：题意   技术   width   class   tree   生成   pac   get   绿色   

$Matrix-Tree$

　　其实矩阵树的题挺好玩的，一些是套班子求答案的，也有一些题目是靠观察基尔霍夫矩阵性质推式子的。

　　文艺计算姬：https://www.lydsy.com/JudgeOnline/problem.php?id=4766

　　题意概述：求完全二分图的生成树数目。左部点的个数为n，右部为m，答案对p取模。$n,m,p<=10^{18}$

　　好玩的题目！刚看到这个题的时候以为是一道板子题，看了一眼数据范围...对于完全二分图，基尔霍夫矩阵是非常有特点的(删掉最后一行最后一列)，首先看对角线，前n行为m，后m-1行为n。右上角和左下角各是一个$ n \times (m-1)$的$-1$块。手动消元一番，发现答案是$n^{m-1}m^{n-1}$，但是消到下半部分只能靠找规律，没有严谨的证明。交上去虽然A了，但是总觉得这个做法不是很靠谱，于是又学了一种非常科学的方法：

　　抛弃原始的按行消元，而是利用特殊的性质。将除第 $n$ 行以外的行加进第 $n$ 行里，此时第 $n$ 行变成这个样子：

　　此时第 $n+1$ 行往下是长这个样子的：

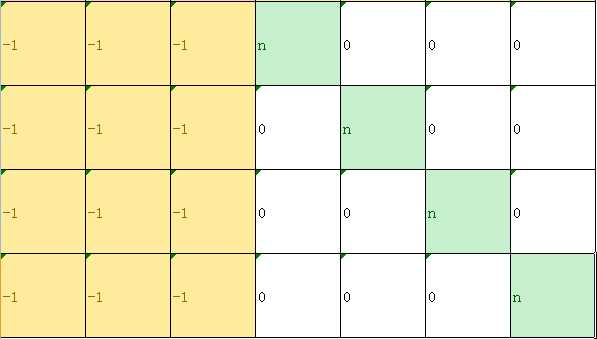
　　把之前消出来的那一行分别加到这些行里面，就只剩下绿色部分了，就像这样：

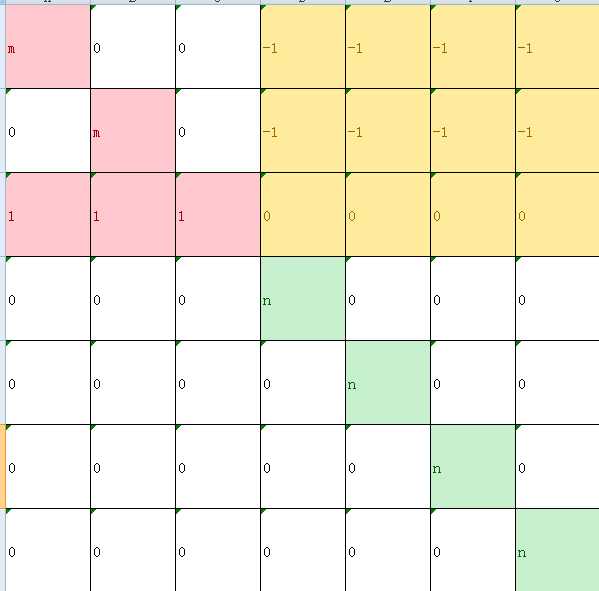
　　问题是这个奇怪的矩阵的行列式怎么求啊？看一看最早的定义式：

　　${det(K)=}\sum_{P}^{ }\;{(}{(-1)}^{\tau{(P)}}\times{K}_{1,p1}\times{K}_{2,p2}\times{K}_{3,p3}\times\cdots\times{K}_{N,pN}{)}$

　　显然每行每列只能选一个数出来，对于前 $n-1$ 列，如果选了 $n$ 行的1，第 $n$ 列就没得选了，所以如果想求有意义的答案，第 $n$ 行必然要选第 $n$ 个数，剩下每行的证明同理，所以这个矩阵的行列式求法等同于上三角矩阵，答案就是 $n^{m-1}m^{n-1}$ 有了准确的证明后感觉非常快乐.

　　

 1 # include <cstdio>
 2 # include <iostream>
 3 # define ll long long
 4  
 5 using namespace std;
 6  
 7 ll n,m,p,ans=1;
 8  
 9 ll mul (ll a,ll b)
10 {
11     ll s=0;
12     while(b)
13     {
14         if(b&1LL) s=(a+s)%p;
15         a=(a+a)%p;
16         b>>=1LL;
17     }
18     return s%p;
19 }
20  
21 ll qui (ll a,ll b)
22 {
23     ll s=1;
24     while(b)
25     {
26         if(b&1LL) s=mul(a,s);
27         a=mul(a,a);
28         b>>=1LL;
29     }
30     return s%p;
31 }
32  
33 int main()
34 {
35     scanf("%lld%lld%lld",&n,&m,&p);
36     ans=mul(ans,qui(m,n-1));
37     ans=mul(ans,qui(n,m-1));
38     printf("%lld",ans);
39     return 0;
40 }

文艺计算姬

---shzr

$Matrix-Tree$定理-题目

标签：题意   技术   width   class   tree   生成   pac   get   绿色   

原文地址：https://www.cnblogs.com/shzr/p/10380548.html