标签:image 分析 ++ 包括 src 解决问题 估计 相关 多项式
时间复杂度估算
因为:
算法=控制结构+原操作(固有数据类型的操作)
所以:
算法的执行时间= 原操作的执行次数*原操作
语句的频度指的是该语句重复执行的次数。
一个算法转换为算法后所耗费的时间,除了与所用的计算软、硬件环境有关外,主要取决于算法中指令重复执行的次数,即语句的频度相关。
一个算法中所有语句的频度之和构成了该算法的运行时间。
例如: for(j=1;j<=n;++j)
for(k=1;k<=n;++k)
++x;
语句“++x、k<=n、++k”的频度是n2,
语句“ j=1、k=1”的频度是1,
语句“j<=n;++j”的频度是n。
算法运行时间为:3*n2+2n+2。
对较复杂的算法计算算法的运行时间,经常从算法中选取一种对于所研究的问题来说是基本(或者说是主要) 的原操作,以该基本操作在算法中重复执行的次数作为算法运行时间的衡量准则。这个原操作,多数情况下是最深层次循环体内的语句中的原操作。
例如: for(i=1;i<=n;++i)
for(j=1;j<=n;++j)
{ c[i,j]=0;
for(k=0;k<=n;++k)
c[i,j]= c[i,j]+a[i,k]*b[k,j];
}
该算法的基本操作是乘法操作,时间复杂度为n3 。
当一个算法的算法运行时间为n2+n+1时,由于n2+n+1与n2的数量级相等(该表达式当n足够大时约等于n2), 我们说这个算法的渐进时间复杂度(简称算法的时间复杂度)为:T(n)=O(n2)。
数量级相等是这样定义的,设f(n)是一个关于正整数n 的函数,若存在一个常数C,使
时间复杂度估算
因为:
算法=控制结构+原操作(固有数据类型的操作)
所以:
算法的执行时间= 原操作的执行次数*原操作
语句的频度指的是该语句重复执行的次数。
一个算法转换为算法后所耗费的时间,除了与所用的计算软、硬件环境有关外,主要取决于算法中指令重复执行的次数,即语句的频度相关。
一个算法中所有语句的频度之和构成了该算法的运行时间。
例如: for(j=1;j<=n;++j)
for(k=1;k<=n;++k)
++x;
语句“++x、k<=n、++k”的频度是n2,
语句“ j=1、k=1”的频度是1,
语句“j<=n;++j”的频度是n。
算法运行时间为:3*n2+2n+2。
对较复杂的算法计算算法的运行时间,经常从算法中选取一种对于所研究的问题来说是基本(或者说是主要) 的原操作,以该基本操作在算法中重复执行的次数作为算法运行时间的衡量准则。这个原操作,多数情况下是最深层次循环体内的语句中的原操作。
例如: for(i=1;i<=n;++i)
for(j=1;j<=n;++j)
{ c[i,j]=0;
for(k=0;k<=n;++k)
c[i,j]= c[i,j]+a[i,k]*b[k,j];
}
该算法的基本操作是乘法操作,时间复杂度为n3 。
当一个算法的算法运行时间为n2+n+1时,由于n2+n+1与n2的数量级相等(该表达式当n足够大时约等于n2), 我们说这个算法的渐进时间复杂度(简称算法的时间复杂度)为:T(n)=O(n2)。
数量级相等是这样定义的,设f(n)是一个关于正整数n 的函数,若存在一个常数C,使
时间复杂度估算
因为:
算法=控制结构+原操作(固有数据类型的操作)
所以:
算法的执行时间= 原操作的执行次数*原操作
语句的频度指的是该语句重复执行的次数。
一个算法转换为算法后所耗费的时间,除了与所用的计算软、硬件环境有关外,主要取决于算法中指令重复执行的次数,即语句的频度相关。
一个算法中所有语句的频度之和构成了该算法的运行时间。
例如: for(j=1;j<=n;++j)
for(k=1;k<=n;++k)
++x;
语句“++x、k<=n、++k”的频度是n2,
语句“ j=1、k=1”的频度是1,
语句“j<=n;++j”的频度是n。
算法运行时间为:3*n2+2n+2。
对较复杂的算法计算算法的运行时间,经常从算法中选取一种对于所研究的问题来说是基本(或者说是主要) 的原操作,以该基本操作在算法中重复执行的次数作为算法运行时间的衡量准则。这个原操作,多数情况下是最深层次循环体内的语句中的原操作。
例如: for(i=1;i<=n;++i)
for(j=1;j<=n;++j)
{ c[i,j]=0;
for(k=0;k<=n;++k)
c[i,j]= c[i,j]+a[i,k]*b[k,j];
}
该算法的基本操作是乘法操作,时间复杂度为n3 。
当一个算法的算法运行时间为n2+n+1时,由于n2+n+1与n2的数量级相等(该表达式当n足够大时约等于n2), 我们说这个算法的渐进时间复杂度(简称算法的时间复杂度)为:T(n)=O(n2)。 数量级相等是这样定义的,设f(n)是一个关于正整数n 的函数,若存在一个常数C,使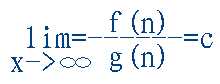
则称f(n)与g(n)是同数量级的函数。
算法(渐进)时间复杂度,一般均表示为以下几种数量级的形式(n为问题的规模,c为一常量):
Ο(1)称为常数级
Ο(logn)称为对数级
Ο(n)称为线性级
Ο(nlogn)
Ο(nc)称为多项式级
Ο(cn)称为指数级
Ο(n!)称为阶乘级
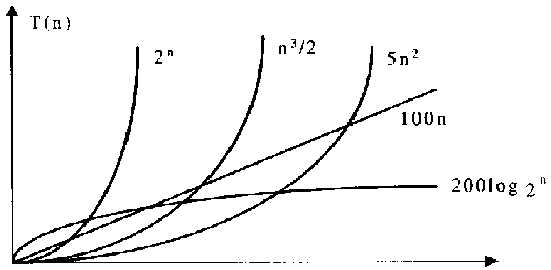
图2-1 T(n)与规模n的函数关系
一般来说如果选用了阶乘级的算法,则当问题规模等于或者大于10时就要认真考虑算法的适用性问题。所以, 原则上一个算法的时间复杂度, 最好不要采用指数级和阶乘级的算法, 而应尽可能选用多项式级或线性级等时间复杂度级别较小的算法。
对于较复杂的算法,可将它分隔成容易估算的几个部分,然后再利用"O"的求和原则得到整个算法的时间复杂度。
例:若算法的两个部分的时间复杂度分别为
T1(n)=O(f(n)) 和 T2(n)=O(g(n)),
则总的时间复杂度为:
T(n)=T1(n)+T2(n)=O(max(f(n),g(n)))。
问题时间复杂度的上界和下界
复杂度的上界和下界是用以估计问题所需某资源的复杂程度的界限函数。如果找到解某问题的算法,其资源的复杂度为u(n), 则u(n)是问题本身复杂度的一个上界。如果对任何算法,其复杂度都必需大于l(n),则l(n)是问题复杂度的一个下界。
定义1:如果存在两个正常数c和n0,对于所有的n=n0,有 |f(n)|≤c|g(n)|,则记作 : f(n)=Ο(g(n))。
定义2:如果存在两个正常数c和n0,对于所有的n≥n0,有|f(n)|≥c|g(n)|,则记作 : f(n)=Ω(g(n))。
定义3:当 f(N)=Ο(g(N)) 且 f(N)=Ω(g(N))时,则记 f(N)=θ(g(N))。也就是说f(N)与g(N)同阶。
定义4:如果对于任意给定的S≥0,都存在非负整数N0,使得当N≥N0时有f(N)≤Sg(N),则称函数f(N)当N充分大时,比g(N)低阶,记为f(N)=o(g(N))。
定义5:若g(N)=o(f(N)), 即当N充分大时, f(N)的阶比g(N)高,则记f(N)=W(g(N))。
5.算法时间复杂度的最好情况和最坏情况
我们要确定能反映出算法在各种情况下工作的数据集, 选取的数据要能够反映、代表各种计算情况下的估算, 包括最好情况下的时间复杂度(时间复杂度下界, 一般记为Tmax)、最坏情况下的时间复杂度(时间复杂度上界, 一般记为Tmin)、平均情况下的时间复杂度(一般记为Tavg)和有代表性的情况, 通过使用这些数据配置来运行算法,以了解算法的性能。
算法的空间复杂性
算法的存储量包括:
1) 输入数据所占空间;
2) 算法本身所占空间;
3) 辅助变量所占空间。
算法的空间复杂度是指算法在执行过程中所占辅助存储空间的大小(也有课本定义为所占全部存储空间的大小), 用S(n)表示。与算法的时间复杂度相同,算法的空间复杂度S(n)也可表示为:
S(n)=Ο(g(n))
表示随着问题规模n的增大, 算法运行所需存储量的增长率与g(n)的增长率相同。
NP完全问题
NP完全性问题属于“计算复杂性”研究的课题。所谓计算复杂性,通俗说来,就是用计算机求解问题的难易程度。其度量标准:
一是计算所需的步数或指令条数(这叫时间复杂度)。
二是计算所需的存储单元数量(这叫空间复杂度)。
问题的复杂性和算法的复杂性的区别:
就时间复杂性说,算法的复杂性是指解决问题的一个具体的算法的执行时间,这是算法的性质;问题的复杂性是指这个问题本身的复杂程度。
如果一个判定性问题的复杂度是该问题的一个实例的规模n 的多项式函数,则我们说这种可以在多项式时间内解决的判定性问题属于P类问题。P类问题就是所有复杂度为多项式时间的问题的集合。通俗地称所有复杂度为多项式时间的问题为易解的问题类,否则为难解的问题。
这种可以在多项式时间内验证一个解是否正确的问题称为NP问题,亦称为易验证问题类。
特殊的NP问题就是NP完全问题(NPC问题,C代表complete)。NPC问题存在着一个令人惊讶的性质,即如果一个NPC问题存在多项式时间的算法,则所有的NP问题都可以在多项式时间内求解,即P=NP成立!! 一般认为NPC问题是难解的问题类。
简单地说,存在多项式时间的算法的一类问题,称之为P类问题,而像梵塔问题、推销员旅行问题等问题,至今没有找到多项式时间算法解的一类问题,称之为NP类问题。
算法分析实例
1.仅依赖于问题规模的时间复杂度
有一类简单的问题,其操作具有普遍性,也就是说对所有的数据均等价地进行处理,这类算法的时间复杂度,很容易分析。
【例1】交换i和j的内容。
Temp=i;i=j;j=temp;
以上三条单个语句的频度均为1,该算法段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶,记作T(n)=Ο(1)。
如果算法的执行时间不随着问题规模n的增加而增长,即使算法中有上千条语句,其执行时间也不过是一个较大的常数。此类算法的时间复杂度是Ο(1)。
【例2】变量计数之一。
(1) x=0;=0;
(2) for(k-1;<=n;++)
(3) x++;
(4) for(i=1;<=n;++)
(5) for(j=1;j<=n;++)
(6) y++;
该算法段的时间复杂度为T(n)=Ο(n2)。
当有若干个循环语句时,算法的时间复杂度是由嵌套层数最多的循环语句中最内层语句的频度f(n)决定的。
【例3】变量计数之二。
(1) x=1;
(2) for(i=1;i<=n;i++)
(3) for(j=1;j<=i;j++)
(4) for(k=1;k<=j;k++)
(5) x++;
该算法段中频度最大的语句是(5),从内层循环向外层分析语句(5)的执行次数:
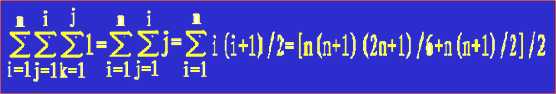
则该算法段的时间复杂度为:T(n)=O(n3/6+低次项)=O(n3)
【例3`】循环次数不是规模的多项式形式。
i=1;
while(i<=n)
i=i*2;
设以上循环的次数为k,则2k=n,所以循环的次数为log2n。
算法的时间复杂度为O(log2n)
标签:image 分析 ++ 包括 src 解决问题 估计 相关 多项式
原文地址:https://www.cnblogs.com/gd-luojialin/p/10381426.html