标签:研究 alt 状态 输入 .com play 时间 code 图片
这部分内容大部分参考W.Y.Choi的课堂讲义第三讲和第四讲:http://tera.yonsei.ac.kr/class/2007_1/main.htm
一、小信号模型
首先要明确一点,大部分情形MOSFET都是工作在饱和区。在饱和区工作的状态我们通常称为静态工作点,在此状态附近考虑一个小的控制信号扰动$v_{GS}$,漏极伴生的附加电流记为$i_D$. 小信号模型就是用于研究这两个物理量之间的关系。
由MOSFET在饱和区的关系$I_D=\frac12\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_T)^2$,关于$V_{GS}$微分,有
$i_D=\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_T)v_{GS}\equiv g_m v_gs$. $g_m=\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_T)=\sqrt{2\mu_nC_{ox}\frac{W}{L}I_D}$.
其中$g_m$就是小信号$i_D$关于$v_{GS}$的电导。小信号电路模型可由下图表示。
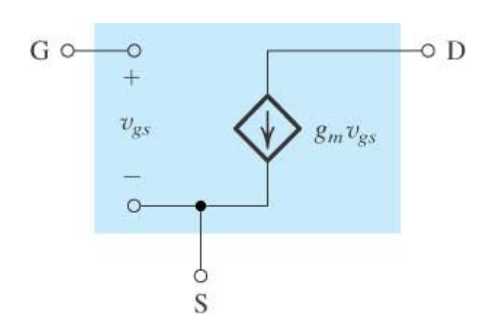
下面考虑沟道长度修正,漏极电流$I_D=\frac12\mu C_{ox}\frac{W}{L}(1+\lambda V_{DS})(V_{GS}-V_T)^2$。由于表达式中有$V_{GS}$,$V_{DS}$两变量,微分变为
$i_D=\frac{\partial I_D}{\partial V_{GS}}v_{GS}+\frac{\partial I_D}{\partial V_{DS}}v_{DS}\equiv g_m v_{GS}+\frac1{r_0}v_{DS}$.
$g_m=\mu C_{ox}\frac{W}{L}(1+\lambda V_{DS})(V_{GS}-V_T)$, $\frac1{r_0}=\frac12\mu C_{ox}\frac{W}{L}\lambda (V_{GS}-V_T)^2$.
受控模型变为:
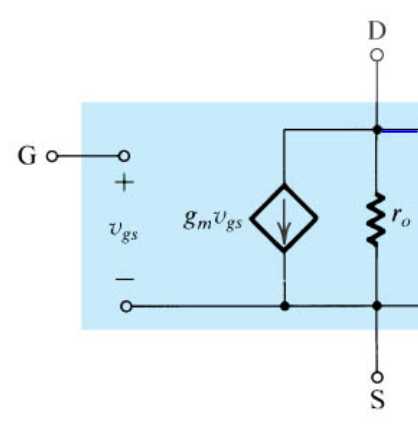
二、MOSFET的频率响应
上面讨论的是MOSFET的直流小信号响应,那么对于含时的信号,我们有必要考虑gate和source间还有gate和drain间的电容,分别记为$C_{GS}$和$C_{GD}$. 它们的来源如下图。
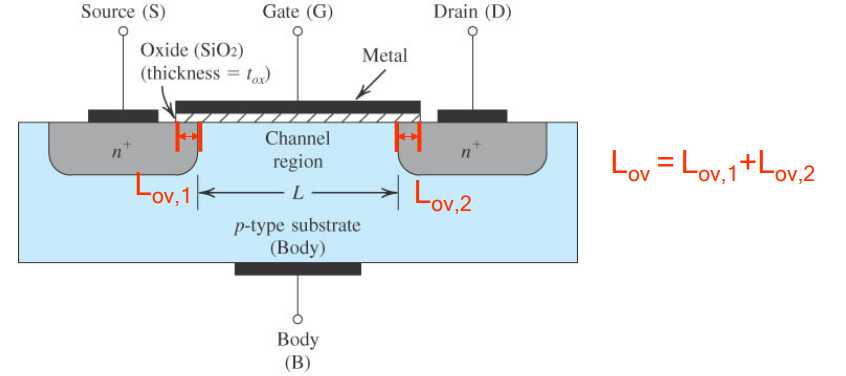
在饱和区,$C_{GS}=\frac23 WLC_{ox}+WL_{ov}C_{ox}$, $C_{GD}=WL_{ov}C_{ox}$. 所以我们有$C_{GS}>C_{GD}$. 注意这里$C_{ox}$的单位很奇怪...
之前直流的小信号模型原电路如下
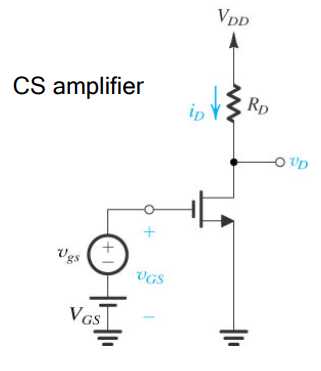
而对于含时信号来说,我们的小信号实际上是对时间微分,故此时$V_{DD}$和$GND$这种不随时间变化的电压源无异。那么漏极电流实际上就是将drain的$V_{DD}$和source的GND相连后流过的电流,即下图中的$I_o$,而输入的小信号是$I_i$.
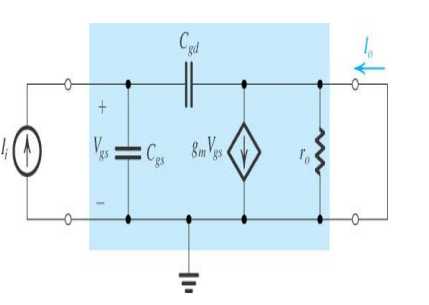
对于频率为$\omega$的情形,$\frac{I_o}{I_i}=\frac{g_m}{j\omega (C_{GD}+C_{GS})}$.
标签:研究 alt 状态 输入 .com play 时间 code 图片
原文地址:https://www.cnblogs.com/zmshum/p/10383030.html