bzoj1367 可并堆

标签：com   code   一半   分析   重复   相等   区间合并   结构   比较   

题面

参考：《左偏树的特点及运用——黄河源》

我们将这个数列划为很多个互不相交的区间，每一段区间内的 \(b\) 是相等的,即

• \(b[l[i]]=b[l[i]+1]=...=b[r[i]]=w[i]?\), \(l[i],r[i]?\) 为区间 \(i?\) 的左右端点

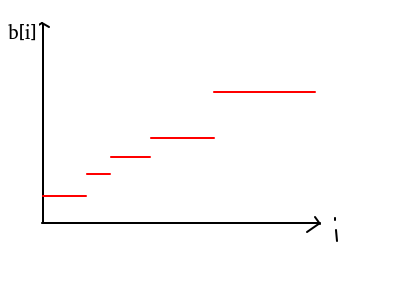
先假设题目时要求b不下降的(比较好讨论),那么答案应该会呈现出这样子：

定理一：对于单个区间的最优解为其中位数，即 \(a[l[i]],a[l[i]+1],...,a[r[i]]\) 的最优解为 \(b[l[i]]=b[l[i]+1]=...=b[r[i]]=\) 中位数。

• 由绝对值的几何意义可得.

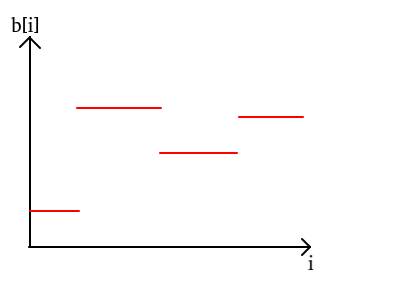
如果我们将"b不下降"这一条件忽略，单纯考虑单个区间的最优解，b可能是这样的：

在讨论如何将不合法的最优解转化为合法的最优解之前，先来了解一些结论：

结论一：对于一段连续的a不下降(可能由多个区间组成)，则 \(b[i]=a[i]\) 时为最优解。

证明：该段绝对值之差为0.

引理一：对于相邻的两个区间 \([l[i]],\ r[i]]\ and\ [l[i+1],\ r[i+1]]?\) , \(u,v?\) 为其最优解，若 \(u\le v?\)， 则 \([l[i],r[i+1]]?\) 的区间最优解为 \(b[l[i]]=b[l[i]+1]=...=b[r[i]]=u,\ b[l[i+1]]=b[l[i+1]+1]=...=b[r[i+1]]=v?\).

证明：子问题最优 -> 整体最优.

引理二：对于相邻的两个区间 \([l[i]],\ r[i]]\ and\ [l[i+1],\ r[i+1]]\) , \(u,v\) 为其最优解，若 \(v < u\) ，则 \(b[r[i]]\le u, v\le b[l[i+1]].\)

画个图：

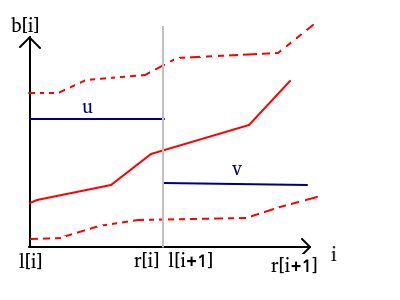
因为除此之外的情况(虚线)一定不会比这种情况更好

如：上面那条虚线没有u+右边部分更优，下面那条虚线没有v+左边部分更优

而u+右边部分与v+左边部分是属于红色折线的.

结论二：对于任意一个序列 \(a[1] , a[2] , ... , a[n]\) ,如果最优解为 \(( u , u , ... , u )\) , 那么在满足\(u ≤ u‘\le b[1] \ or \ b[n] \le u‘ ≤ u\) 的情况下,\(( b[1] , b[2] , ... , b[n] )\) 不会比 \(( u′ , u′ , ... , u′ )\)更优。

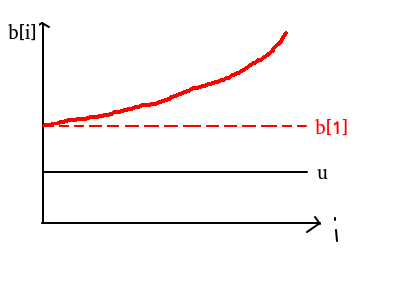
给出 \(u\le u‘\le b[1]\) 的证明，后者类似可证.

证明：

对于 \(n=1，a[1]=u,?\) 显然成立.

假设对于n是成立的，那么将 \(b[1],b[2]...b[n],b[n+1]\) 都设为 \(b[1]\) , 若解变得更坏了，则最优解应该是 \((u,u,...,u,b[n+1])\) 而不是 \((u,u,...u,u)\), 而由几何意义得 \((b[1],b[1]...b[1])\) 比 \((u‘,u‘,...,u‘)\) 会差，故对于 \(n+1\) 也成立.

由数学归纳原理可得命题成立.

至此，我们已经可以将局部最优解合成整体最优解了!

一：

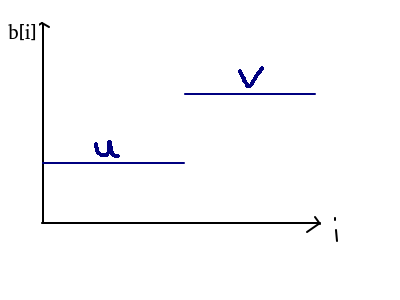
u，v为两段区间的最优解，由引理一全局最优解为 \((u,u,...,u,v,v,...,v)\).

二：

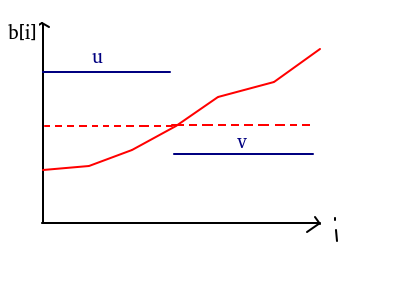
这种情况较为复杂，由引理二可得最优解一定是左边\(\le u\), 右边的 \(\geq v\)，即为红色部分，

又由结论二得虚线部分比红色部分更优(其实是不会更差), 所以这个整个区间的最优解一定为一个定值!

注：其实左边的虚线是比右边低的，但是左边的虚线越往上越优，右边的虚线越往下越优，故最优时它们高度相同，为一定值。

接下来就转换成求这个定值了。

由定理一，值该定值即为整个数列的中位数!!

所以一开始假设每个数就是一个区间，然后不断合并区间，最终知道全局最优解。

• 假设我们已经找到前 \(k\) 个数 \(a[1], a[2], ... , a[k] (k<n)\) 的最优解,
• 得到 \(m\) 个区间组成的队列, 对应的解为 \((w[1], w[2] , ... , w[m])\),
• 现在要加入 \(a[k+1]\), 并求出前 \(k+1\) 个数的最优解。
• 首先我们把 \(a[k+1]\) 作为一个新区间直接加入队尾,令 \(w[m+1]=a[k+1]\) ,
• 然后不断检查队尾两个区间的解 \(w[m]\) 和 \(w[m+1]\),如果 ?\(w[m] > w[m+1]\) ,
• 我们需要将最后两个区间合并,并找出新区间的最优解(也就是序列 \(a?\) 中,下标在这个新区间内的各项的中位数)。
• 重复这个合并过程,直至 \(w[1] ≤ w[2] ≤ ... ≤ w[m]?\) 时结束,然后继续处理下一个数。
• 画图理解...

现在我们需要考虑一下数据结构的选取,

算法中涉及到以下两种操作:

1.合并两个有序集

2.查询某个有序集内的中位数

我们很容易想到平衡树，但是就算是启发式合并，复杂度也有 \(O(nlog^2n)?\), \(1e6?\) 过不了.

我们可以用大根堆来维护每个区间内的中位数，我们发现右端的堆都是单个元素的加入，只要一下降，就会合并，所以合并是正确的。

“通过进一步分析,我们发现,只有当某一区间内的中位数比后一区间内的中位数大时,合并操作才会发生,也就是说,任一区间与后面的区间合并后,该区间内的中位数不会变大。于是我们可以用最大堆来维护每个区间内的中位数,当堆中的元素大于该区间内元素的一半时,删除堆顶元素,这样堆中的元素始终为区间内较小的一半元素,堆顶元素即为该区间内的中位数。” —— 黄源河

堆顶元素即为该区间内的中位数。

考虑到我们必须高效地完成合并操作,左偏树是一个理想的选择,每个操作都是 \(O(logn)\),

总时间复杂度 \(O(nlogn)?\).

bzoj1367 可并堆

标签：com   code   一半   分析   重复   相等   区间合并   结构   比较   

原文地址：https://www.cnblogs.com/HNYLMSTea/p/10386117.html