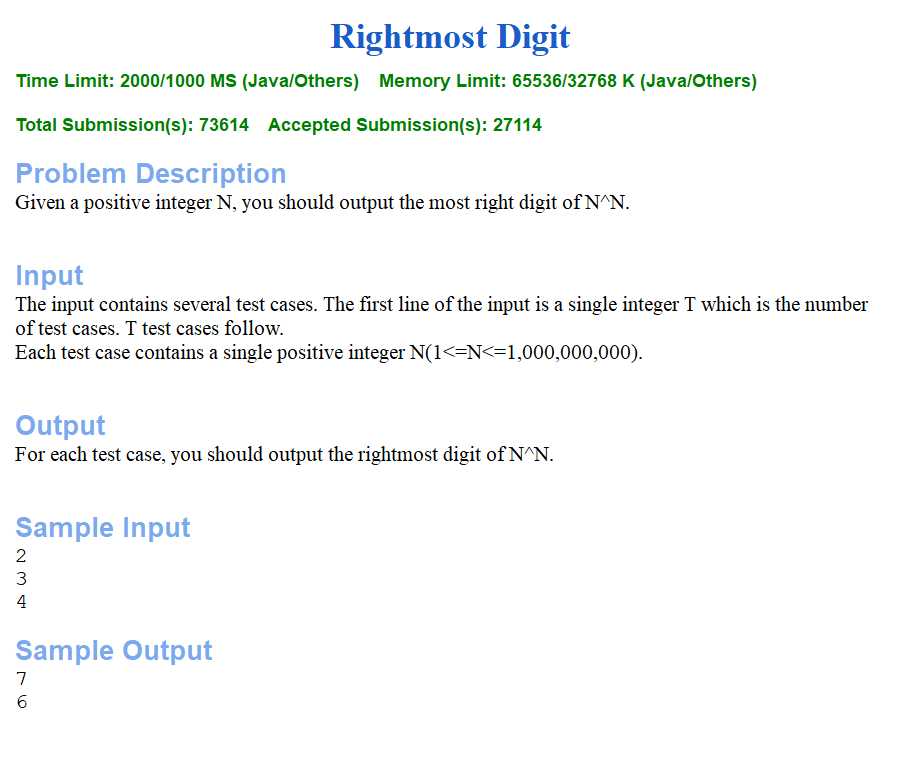
标签:pre for clu 需要 pua 快速 class bottom 代码


数据级别在1,000,000,就正常做不会超时,最简单的快速幂,根据 (a * b) % p = (a % p * b % p) % p
测试链接:http://acm.hdu.edu.cn/showproblem.php?pid=1021
#include <iostream> #include <stdio.h> using namespace std; int main(){ int n; while(scanf("%d",&n)!=EOF){ int f0=7,f1=11; int fn; for(int i=2;i<=n;i++){ fn=(f0+f1)%3; f0=f1%3; f1=fn%3; } if(n<=1){ cout<<"no"<<endl; } else{ if(fn%3==0) cout<<"yes"<<endl; else cout<<"no"<<endl; } } return 0; }
数据级别10亿,上一种就无法完成了,需要用另一种方法降低 n 的规模。
原理:比如 a^7=a^4*a^2*a^1=(a^2*a^2)*(a^1*a^1)*a^1。简单来说,就是求过的 a^i 的值不再求一遍,拿来直接用。
测试链接:http://acm.hdu.edu.cn/showproblem.php?pid=1061
式子中%号尽量多写,反正多写不会错,少写说不定超范围了,这是O(logn)级别的,10^9也不过就是30多次,不用担心时间的问题。
#include <iostream> using namespace std; int main() { int N; cin >> N; while (N--) { int n, res = 1; cin >> n; int a = n; while (n) { if (n & 1) { res = ((res % 10) * (a % 10)) % 10; } a = ((a % 10) * (a % 10)) % 10; n /= 2; } cout << res << endl; } return 0; }
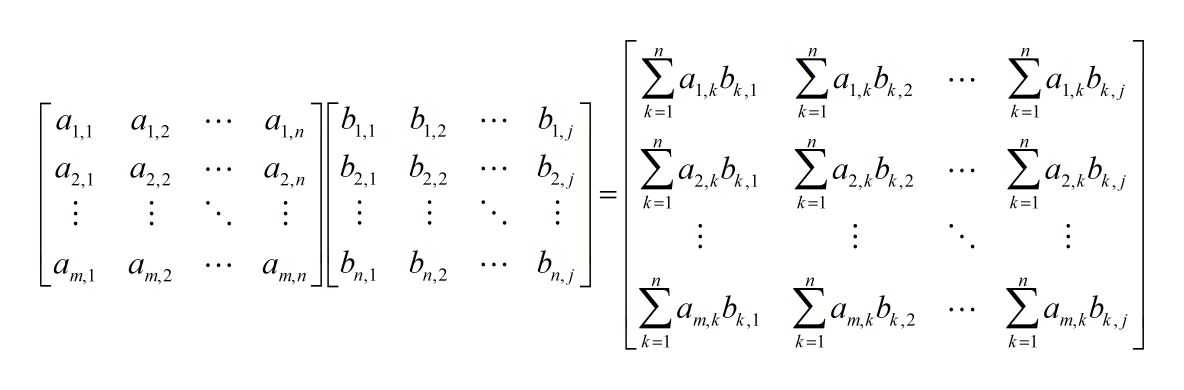
对着例子好理解些:
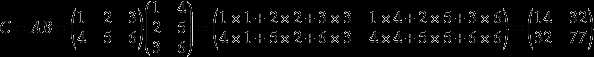
要注意的是:A的行数与B的列数必须相同才可以进行乘法
矩阵乘法:
//A :m行*n列;B:n行*m列 int** MatMulti(int **A, int **B, int m, int n) { int **C = new int*[n + 1]; for (int i = 1; i <= n; i++) { C[i] = new int[n + 1]; memset(C[i], 0, sizeof(int)*(n + 1)); } for (int i = 1; i <= m; i++) { for (int j = 1; j <= m; j++) { for (int k = 1; k <= n; k++) { if (A[i][k] == 0 || B[k][j] == 0)continue; C[i][j] += A[i][k] * B[k][j]; } } } return C; }
完整测试代码:

#include <iostream> using namespace std; //A :m行*n列;B:n行*m列 int** MatMulti(int **A, int **B, int m, int n) { int **C = new int*[n + 1]; for (int i = 1; i <= n; i++) { C[i] = new int[n + 1]; memset(C[i], 0, sizeof(int)*(n + 1)); } for (int i = 1; i <= m; i++) { for (int j = 1; j <= m; j++) { for (int k = 1; k <= n; k++) { if (A[i][k] == 0 || B[k][j] == 0)continue; C[i][j] += A[i][k] * B[k][j]; } } } return C; } /*2 3 1 2 3 4 5 6 1 4 2 5 3 6*/ int main() { int **a, **b; int m, n; cin >> m >> n; a = new int*[m + 1]; b = new int*[n + 1]; for (int i = 1; i <= m; i++) { a[i] = new int[n + 1]; } for (int i = 1; i <= n; i++) { b[i] = new int[m + 1]; } for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { cin >> a[i][j]; } } for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { cin >> b[i][j]; } } int **c = MatMulti(a, b, m, n); for (int i = 1; i <= m; i++) { for (int j = 1; j <= m; j++) { cout << c[i][j] << " "; } cout << endl; } return 0; }
哪里该用m,哪里该用n搞不太清除也没关系,矩阵快速幂只会用到方阵。
标签:pre for clu 需要 pua 快速 class bottom 代码
原文地址:https://www.cnblogs.com/czc1999/p/10111573.html