标签:目标 .com 写法 return oid rate 怎么 rom gic
首先明白一个概念,什么是逻辑回归;所谓回归就是拟合,说明x是连续的;逻辑呢?就是True和False,也就是二分类;逻辑回归即使就是指对于二分类数据的拟合(划分)。
那么什么是模型呢?模型其实就是函数。函数是由三部分组成:自变量,因变量以及参数。
此次采用模型是sigmoid函数:
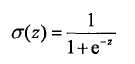
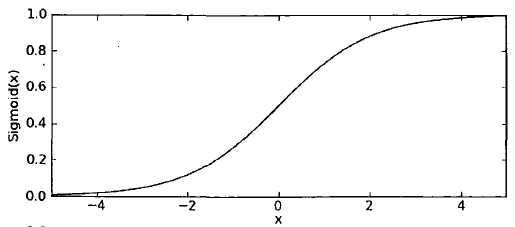
sigmoid函数的精妙之处就在于在x=0点出是一个分水岭,x>0y值去1,x<0 y值取0。所以sigmoid函数很像是跃阶函数。
z代表什么?则代表分类的数学表达式,是函数的右侧;
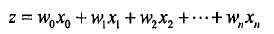
那么怎么使用sigmoid阶函数?sigmoid函数目标情况是当传入z,返回值是1或者0;但是实际情况因为参数(w0,w1..wn)都是估计状态,基本都是不为0,1;通过样本分类(0,或者1)和sigmoid值相减,获取一个差量,下面就是调整参数(weight),让数据不断合理;
from numpy import mat from numpy import shape from numpy import ones def gradientAsendent(dataset, labels, time): dataMat=mat(dataset) labelMat=mat(labels).transpose() m,n=shape(dataMat) weights=ones((n,1)) #这个写法(两层括号)是创建一个矩阵 alpha=0.001 #学习率rate maxtimes=time for i in range(maxtimes): #sigmod函数解决的分类问题,dataMat*weights返回的是一个矩阵,行数=datamat,列数=weights h=sigmod(dataMat*weights) # 合心意应该error=0,h应该是0,1的数组;但是sigmod返回的分类一定不是正好0,1,而是有差距的 # 目标就是通过调整系数(weights)来减少减少error的和0的差距,也是让h里面的数据不断的接近0,1 error=(labelMat - h) # 如果有偏差了,就添加/减小参数值 weights=weights+alpha*dataMat.transpose()*error
return weights
标签:目标 .com 写法 return oid rate 怎么 rom gic
原文地址:https://www.cnblogs.com/xiashiwendao/p/10390619.html