红黑树的理解与学习+伪代码

标签：过程   移动   相关   查找   左旋转   转变   lse   不能   style   

在看HashMap源码的时候，涉及到红黑树，这个数据结构早已听闻大名，而且在学校的教材中没有讲这个数据结构，所以花了点时间去学习和理解这个数据结构。（比我想象中的复杂的多……）

Red-Black Tree的简介

首先这是个二叉查找树，它属于但又不严格属于平衡二叉树（AVL），因为它没有像平衡二叉树一样，严格规定平衡因子的绝对值要小于等于1，而是靠他的颜色规定来达到高性能。

一棵拥有n个元素的RB树，树的高度最多为2log(n + 1)，所以操作的时间复杂度是O(logN)级别的。——所以它其实是一棵平衡查找树。

RB-Tree的properties

首先，红黑树看名称我们都知道，这是个带颜色的树。

红黑树有五个设定，或者说是规矩/性质：

1. 每个结点，要么是红色，要么是黑色。
2. 根节点是黑色的。
3. 每个叶节点，或者说是NIL节点（也可以说是null空结点）都是黑色的。
4. 如果一个结点是红色的，那么它的爸爸不能是红色，它的子女也不能是红色，总之红黑树中不允许连续的两个红色结点出现。
5. 对于每个结点，从该结点到其后代的所有叶节点的简单路径上，均包含相同数目的黑色节点。

还有两个小概念：

1. 为了方便处理边界条件以及方便描述，我们把不需要关注的叶子节点和null节点统一用一个特殊节点表示，我们称它为哨兵节点，记为T.NIL。
2. 第五点性质也能用一个叫做黑高——Black height的概念来描述——从某个节点x出发（不含该节点）达到一个叶节点的任意一条简单路径上的黑色节点个数称为该节点的黑高。

这里有时候作图方便，用两个圈圈来表示红色的节点，一个圈来表示黑色的节点。

下面看个红黑图的例子：

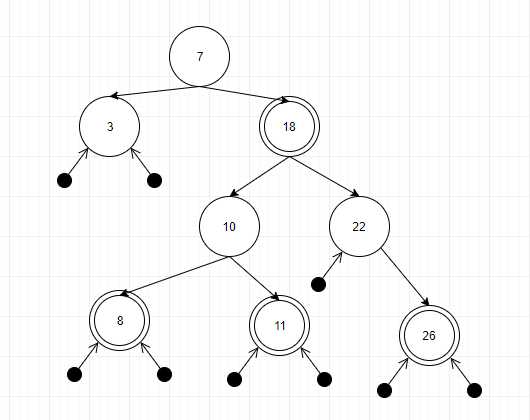
8节点是个红色节点，它的黑高为1；3的黑高也是1；10的黑高也是1。

就是因为这么苛刻看起来很奇怪的需求，让红黑树有了相当不错的性能。

红黑树的插入

首先，红黑树是一棵二叉查找树，所以首先的插入操作和一般的插入查找树一样，根据查找树的规矩将节点插入到正确的位置。

插入后，该新新节点便出现在叶子的位置，然后我们要上色——上成红色。

为什么是红色呢？红黑树的插入的难点就是要维持住那五个性质，如果你插入的是黑色，毫无意义第5条规矩肯定会被破坏掉。而如果插入的是红色，则存在规矩仍然成立的情况。

这个时候，我们很可能破坏了红黑树的规矩了，比如规矩4——连续两个红色节点。（其实好像也只可能破坏规矩4）

然后我们要做的，是如果发现冲突，则把这个冲突往上移动。

往上移动是总体的一个思路，相关的做法是：我们需要通过对一些节点进行从新上色，从而将破坏规矩的冲突位置往上移动，直至可以通过旋转来解决，旋转解决的过程中很可能伴随着再要重新上色。

说明下，伪代码中的节点里的P代表是父亲，然后left和right就分别代表左孩子和右孩子。

看下伪代码：

RB-INSERT(T, x)
  y = T.NIL;
  z = T.root;
  // 一直循环直到找到z的合适位置
  while z != T.NIL
    y = z;
    if x.key < z.key
       z = z.left;
    else z = z.right;
  x.p = y;
  if y == T.NIL
     T.root = x;
  elseif x.key < y.key
     y.left = x;
  else y.right = x;
  x.left = T.NIL;
  x.right = T.NIL;


  //这上面都是二叉查找树的插入过程，重点看下面

  //为新插入的节点上色成红色
  x.color = RED;
  
  //如果红色的新插入节点x的爸爸也是红色，就和规矩四冲突了，就要调整恢复红黑树的五大性质
  if(x.p.color == RED)RB-INSERT-FIXUP(T, x);

插入上色后，因为x为红色，所以只是可能与规矩4冲突，所以只要检测到x的爸爸是红色，就要调用恢复函数。

恢复函数的大致思路：

因为爸爸已经是红色了嘛，然后思路就是主要研究爷爷，还有爸爸的兄弟。爷爷这里其实已经知道了，一定是黑色的，因为爸爸是红色的话，爷爷只能是Black。

代码的思路是，不断地从新节点将冲突往上走，所以首先有个循环，只要x不是root根结点，x还是红色，循环就继续。

然后对于每个x，我们分为两个categoryA还有categoryB两个大情况，其实就是x的父亲是爷爷的左孩子还是右孩子，这两个category的操作是刚好相反的，然后这里的伪代码就只是写出一个。

然后每个category里面又有三种case。

case1：

　　爷爷是Black（肯定），然后叔叔是红色的。这个时候我们只要把爷爷由黑色变成红色，然后把叔叔和爸爸都变成黑色，这样局部也就是从爷爷开始看下来，是没有冲突的，但爷爷由黑色变成红色肯定会造成上面的冲突，这里就把冲突往上移动了。所以，下一步就是把x赋值为爷爷，继续循环。

（图片是借https://blog.csdn.net/lm2009200/article/details/70148565的，所以上面说的case2不关事hh）

case2：

　　叔叔是黑色的，x是爸爸的右孩子，先假设爸爸是爷爷的左孩子（就假设某个category）。然后视觉上，x和爸爸的红色冲突是“z”型的，这个时候需要的操作是对x进行左旋，然后就会把冲突变到一条直线上哈哈。

然后就可以进入case3.

（图片是借的，所以上面的case是不一样的hh）

case3：

　　叔叔是黑色的，x是爸爸的左孩子，假设爸爸是爷爷的左孩子。这就冲突在一条线上了，这里涉及的操作是既要旋转也要上色，这里也借一下大佬的图片：

（同样无视里面的case的字）

要做的是，对x的爸爸进行右旋转，然后并对x的爸爸z重上色；还有对x的爷爷a重上色。

case4是终结情况，然后x要移动到它爸爸也就是z的位置，然z不是红色，循环结束。

这是别人写的一个解析：

我们一步步的分析如何从左边的图调整为右边的图，首先还是回到我们的指导思想，把x指针指向节点的父节点染黑，染黑后发现改变了子树Q和W的黑高，那么一个做法就是右旋转a节点，右旋节点a后发现子树F和G的黑高加了1，破坏了性质5，那么把节点a染红，正好就把黑高调整回来了，经过这样的调整，也就变成了上面右边的红黑树图案了。至此，性质4恢复了，红黑树的插入调整也正常结束。

然后看调整算法的伪代码：

while(x != T.root && x.color == RED) {
    if（x.p == x.p.p.left） {
    //x的爸爸是爷爷的左孩子，categoryA
        
        y == x.p.p.right;//y是爷爷的右孩子，也就是x的叔叔
        if（y.color == red）{
            //case1的情况
        
            x.p.color = black;
                  y.color = black;
                  x.p.p.color = red;
                  x = x.p.p;
        } else {
          //x的叔叔不是红色，分成case2和case3

            if(x == x.p.right) {
            //case2——冲突成z型
        
                x = x.p;
                LEFT-ROTATE(T, x);//左旋转操作

                //然后就变成case3
            }

            //case3 选择加变色
            x.p.color = black;
                x.p.p.color = red;
                RIGHT-ROTATE(T, x.p.p);
        }
    
    } else(x.p为右子树，也就是x的爸爸是爷爷的右孩子，和爸爸是左孩子的操作相反即可);
  
}
T.root.color = BLACK;//如果一查入就是根节点，就直接到这里但根节点还是红色，所以要变成黑色。

红黑树的删除

删除就特么复杂了。

首先先来复习一下，二叉查找树的删除操作：

　　如果要删除的那个结点没有孩子，直接删除；如果要删除的节点有一个左孩子或者右孩子，那么就由这个孩子来代替它；如果要删除的节点有两个孩子，那么要找它的直接前驱，它可以是左子树的最右边（比它小的最大值），也可以是右子树的最左边（比它大的最小值），找到直接前驱后，将直接前驱覆盖到要删除的节点的位置，然后删除直接前驱——问题转换到情况2甚至情况1。

红黑树的删除的大致流程也和这个差不多，但它要恢复红黑树的五条性质。

首先我们为红黑树定义一个覆盖函数：

//替换函数，用v节点替代u，只负责更改父节点的指向，左右孩子需要自己更改
RB-TRANSPLANT(T, u, v) {
    if(u.p == null) {
        T.root = v;    
    } else if(u == u.p.left) {
        u.p.left = v;    
    } else u.p.right = v;

    v.p = u.p;
}

然后是红黑树的删除流程函数的伪代码：

RB-DELETE(T, z)
  y = z;
  y-original-color = y.color;
  if z.left == T.NIL
    x = z.right;
    RB-TRANSPLANT(T, z, z.right);
  else if z.right == T.NIL
    x = z.left;
    RB-TRANSPLANT(T, z, z.left);
  else y = TREE-MINMUM(z.right)
    y-original-color = y.color;
    x = y.right;
    if y.p = z;
      x.p = y;
    else RB-TRANSPLANT(T, y, y.right)
         y.right = z.right; 
         y.right.p = y;
    RB-TRANSPLANT(T, z, y)
    y.left = z.left;
    y.left.p = y;
    y.color = z.color;//更改y的颜色,这样的话从y以上红黑树的性质都不会违反 
  if y-original-color == black
    RB-DELETE-FIXUP(T, x)

一开始看这个有点绕，因为以前写二叉查找树的删除，涉及替换是把要删除的那个点的值用直接前驱的值覆盖上去，然后改为删除直接前驱，而这里是直接通过指针的移动，反正如果不拿着笔仔细画指针很容易懵。

z指的一直是要删除的那个点，通过指针的移动后，z指的点会不可达（这里少了free节点z的操作），也就是被删除了；

y指的是，理论上真正要删除的这个点，这里就是懵的地方，后面才看清楚这里的指针，比如本来要删除z，然后找了z的直接前驱，理论上，直接前驱的值被覆盖到z上，然后删除直接前驱，所以y指向这个直接前驱。但这里指针的操作是，直接把y指向的直接前驱变到z的位置上，z变成没有爸爸，即不可达。所以这种情况删除完毕，y所指的节点还在树上；

x指向的，节点被删除后，补上那个空位的节点。

上面的几种删除情况用借一个大佬的示意图来理解：

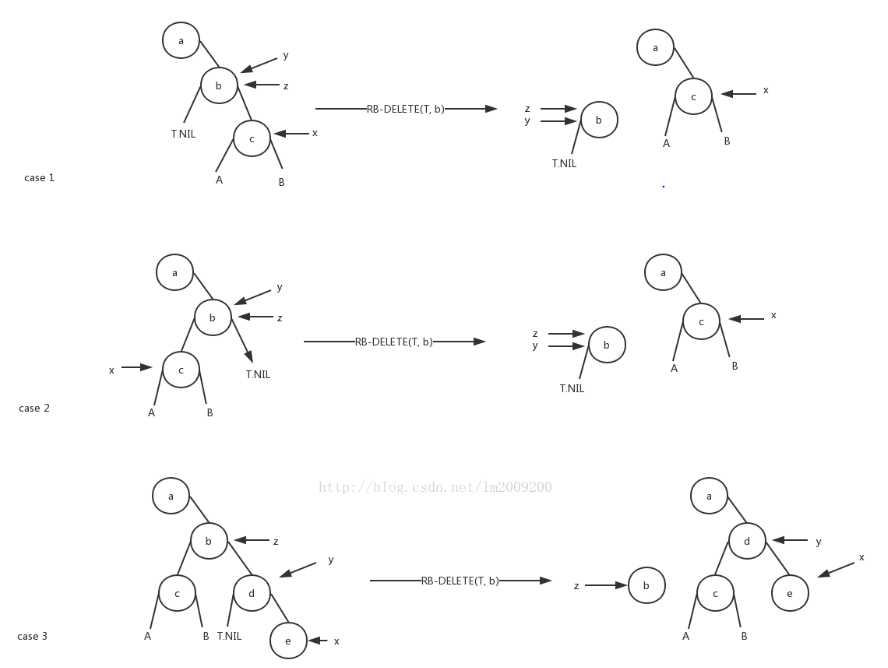
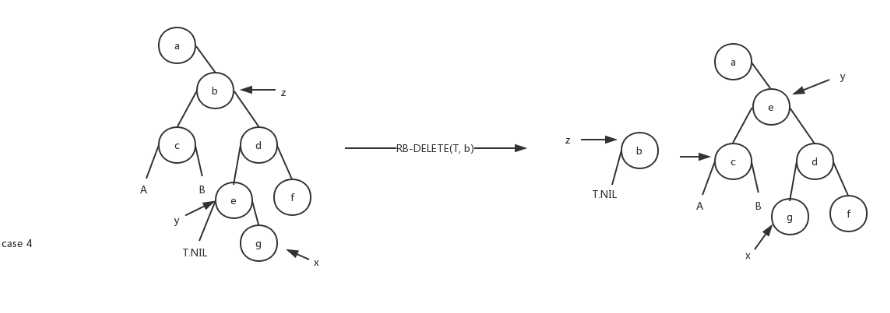
首先，如果被删除的那个，也就是上图左边y指向的那个，或者说理论上要删除的那个节点是红色，那么对那五条性质不会有影响，只有这个被删掉的y是黑色的，才需要调用下面的恢复函数。

恢复思路：

首先，被删除的那个是黑色，那么百分之白含有这个节点的路径的黑高会见一，也就是肯定违背性质5，在已知这个的情况下，再分下面几种情况（下面的情况都是已经违背了性质5）：

1. 违背性质2，如果被被删除的那个是根节点，而它的唯一一个孩子是红色的节点，那么就违背性质2了，这个很容易解决，直接把根节点染黑就行了。

2. 违背性质4，也就是x为红色，他爸也是红色，这种情况也容易解决，因为我们黑高是少了一的嘛，所以我们可以直接染黑x，这样刚好解决问题。

3. 剩下的情况，就是只是违背了性质5了，只要调整好性质5就行了。

这里有一个技巧，就是把x节点视为还有一层黑色，问题就变成了解决违反性质1了，也就是把x看成既红又黑，我们只要把这层额外的黑色不断往上推，直到推给了一个红色节点，那么子树的黑高就恢复了。和插入一样，有个关键思想是，转换过程中千万不能破坏其他任何的性质。经过分析，破坏性质1（本质上是破坏性质5）有以下五种情况：

只是违背性质5的情况下的五种情况：

以下内容全来自博客：https://blog.csdn.net/lm2009200/article/details/70162811

case 1 x是红色的

case 2. x的兄弟节点w是红色的

case 3 x的兄弟节点w是黑色的，而且w的两个子节点都是黑色的

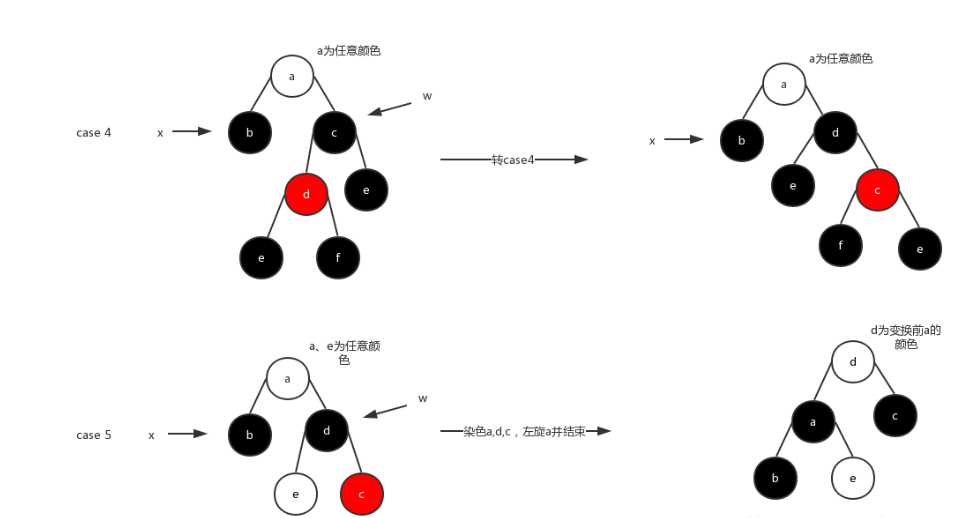
case 4 x的兄弟节点w是黑色的，w的左儿子是红色的，w的右孩子是黑色的

case 5 x的兄弟节点w是黑色的，且w的右孩子是红色的。

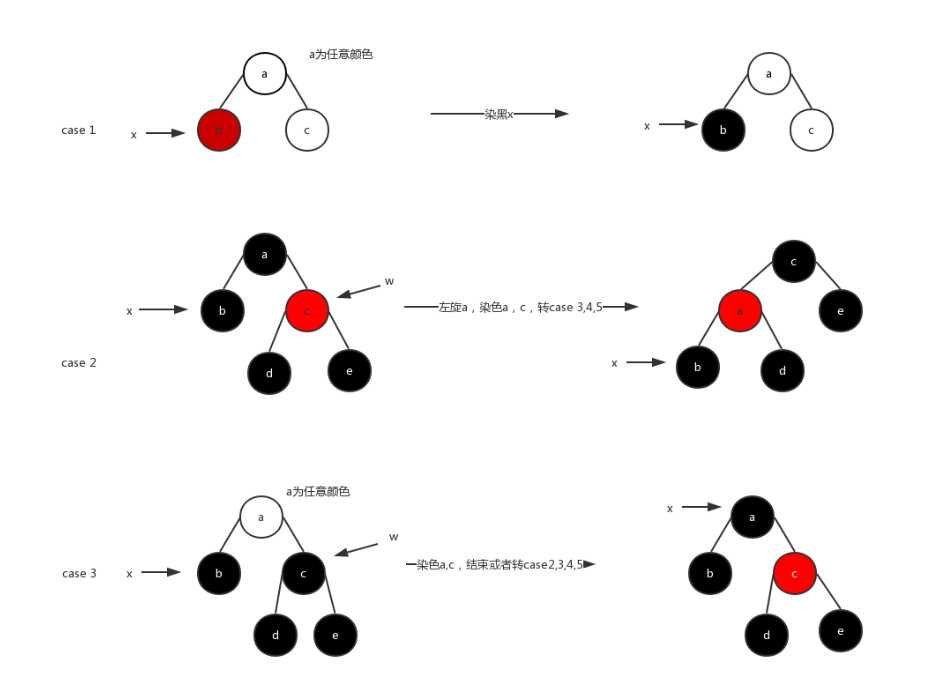
case 1是最容易解决的，直接染黑就是了。也就是说，违背性质4的情况可以和这里归为一类，都是直接染黑x。

case 2的话，改变w和x.p的颜色，左旋转x.p，这样子不改变任何性质的同时，把case 2转变为case 3，4，5。不做详细讨论
伪代码为：

w.color = black;

x.p.color = red;

LEFT-ROTATE(T, x.p)

w = x.p.right;

case 3的话，可以认为从x和w去掉一层黑色给x.p，如果x.p为原本为红色的话，那么x的子树黑高加一，w子树黑高不变，性质就恢复好了，如果x.p原来为黑色的，那么认为x.p的整个子树黑高都少了1，多了的一层黑色就给了x.p，case3就转为case 2,3,4,5了。

伪代码如下：

w.color = red;
x = x.p

case 4的情况左侄儿为红，右侄儿为黑，这种情况统一转case 5来处理。

这里右旋w并且没有改变红黑树的五大性质，转为了case5。伪代码如下：

w.left.color = black;
w.color = red;
RIGHT-ROTATE(T, w)
w = x.p.right;

case 5的情况是红黑树调整的出口，只要到达了case 5，调整完就能恢复所有性质了。调整如下图所示： 

接下来分析case5的转换过程，这里的思路是这样的：首先我们要让x子树黑高加一，那么就左旋转a，左旋转后d的左子树没有任何问题，但是右子树黑高可能减少了1（如果a原来是黑色的情况），为了解决这个问题，可以把a和d颜色交换，然后染黑c，这样左旋转后的d的右子树的黑高也就不会有任何改变了。伪代码如下：

w.color = x.p.color;
x.p.color = black;
w.right.color = black;
LEFT-ROTATE(T, x.p);
x = T.root;

最后是整个删除调整的伪代码：

RB-DELETE-FIXUP(T, x)
 while x != T.root && x.color = black
   if x == x.p.left
     w = x.p.right
     // case 2
     if w.color = red
       w.color = black;
       x.p.color = red;
       LEFT-ROTATE(T, x.p)
       w = x.p.right;
     // case 3
     if w.left.color == black && w.right.color == black
       w.color = red;
       x = x.p;
     // case 4
     else if w.right.color == black
       w.left.color = black;
       w.color = red;
       RIGHT-ROTATE(T, w)
       w = x.p.right;
     // case 5
     w.color = x.p.color;
     x.p.color = black;
     w.right.color = black;
     LEFT-ROTATE(T, x.p);
     x = T.root;

 参考文章与资料：

　　网易云公开课的算法导论红黑树部分。

　 《必须要把红黑树讲清楚，看完还不明白请直接找我之》

　　　　系列2——https://blog.csdn.net/lm2009200/article/details/70148565

　　　　系列3——https://blog.csdn.net/lm2009200/article/details/70162811

红黑树的理解与学习+伪代码

标签：过程   移动   相关   查找   左旋转   转变   lse   不能   style   

原文地址：https://www.cnblogs.com/wangshen31/p/10393317.html