标签:主席树 技术 log http code com class height string

论文中的解法是离线插入 \(O(\log n)\) 询问 \(O(\log n)\) 的,不过我发现有一种离线插入 \(O(1)\) 询问 \(O(\log n)\) 的方法。
首先我们离线处理,将两个串连在一起。我们以 \(ababa\) 和 \(aba\) 为例:

比如现在我们要询问 \(A\) 串 \([1,4]\) 和 \(B\) 串 \([1,2]\)
我们先在 \(rnk[7]\) 开始倍增,使得 \([l,r]\) 中 \(height>=2\)
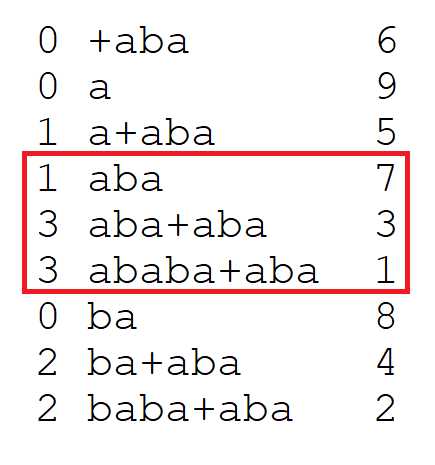
然后我们在这个区间中找多少 \(1\leq sa[i]\leq 3\)。为什么是 \(3\) 呢?因为 \(3-4-len_b+1\)。显然答案为 \(2\)
询问就是主席树上区间加,询问是 \(O(\log n)\) 的,插入是 \(O(1)\) 的。
标签:主席树 技术 log http code com class height string
原文地址:https://www.cnblogs.com/owencodeisking/p/10395258.html