标签:its image 复杂 lse pow quic nbsp 时间复杂度 题意
传送门:Educational Codeforces Round 60 – D
给定N,M(n <1e18,m <= 100)
一个magic gem可以分裂成M个普通的gem,现在需要N个gem,可以选择一定的magic gem,指定每一个分裂或不分裂,问一共有多少种方案
两种分裂方案不同当且仅当magic gem的数量不同,或者分裂的magic gem的索引不同。
1.首先从dp的角度出发
设F(i)为最终需要i个gem的方案数,容易得到递推式:
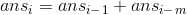
(总方案数 = 最右边的magic gem分裂得到的方案数 + 最右边的magic gem不分裂得到的方案数)
2.观察数据范围可以看到,如果直接这样计算,时间复杂度是要上天的
我们可以把递推式求解转化成矩阵乘法求解
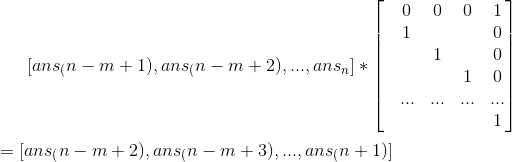
3.套用矩阵快速幂的板子,加速计算
参考代码:
#include <bits/stdc++.h> using namespace std; typedef long long ll; #define _____ ios::sync_with_stdio(false);cin.tie(0); const int M = 1e9 + 7; //head ll n,m; struct Mat{ ll a[102][102]; }; Mat mul(const Mat & a,const Mat & b){ Mat ans; for(int i = 1; i <= m; i++){ for(int j = 1; j <= m; j++){ ans.a[i][j] = 0; for(int k = 1; k <= m; k++){ ans.a[i][j] += a.a[i][k]*b.a[k][j]; if(ans.a[i][j] > M)ans.a[i][j] %= M; } } } return ans; } Mat quick_pow(Mat a,ll b){ Mat t; for(int i = 1; i <= m; i++)t.a[i][i] = 1; while(b){ if(b & 1)t = mul(t,a); b >>= 1; a = mul(a,a); } return t; } int main(){ //freopen("data.in","r",stdin); _____ cin >> n >> m; if(n < m){cout << 1 << ‘\n‘;} else{ Mat ans,t; for(int i = 1; i < m; i++){ ans.a[i+1][i] = 1; } ans.a[1][m] = ans.a[m][m] = 1; ans = quick_pow(ans,n-m); Mat a; for(int i = 1; i < m; i++)a.a[1][i] = 1; a.a[1][m] = 2; a = mul(a,ans); cout << a.a[1][m] << ‘\n‘; } return 0; }
[递推+矩阵快速幂]Codeforces 1117D - Magic Gems
标签:its image 复杂 lse pow quic nbsp 时间复杂度 题意
原文地址:https://www.cnblogs.com/fanwl/p/10411586.html