标签:value image 表示法 精度 not nbsp 额外 两种 ber
若想了解float的组成及计算,我们需要先了解原码、补码、和反码的概念。
一、原码、反码、补码(计算机中的符号数有三种表示方法)
1.原码:原码(true form)是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小。
原码的缺点:原码是有符号数的最简单的编码方式,便于输入输出,但作为代码加减运算时较为复杂
2.补码:在计算机系统中,数值一律用补码来表示和储存。原因在于,使用补码时,可以将符号和数值域统一处理。此外,补码与原码互相转换,其运算过程时相同的,不需要额外的有硬件电路。
特性:
(1)一个负整数(或原码)与其补数(或补码)相加,和为模(“模”实质上是计量器产生“溢出”的量)。
(2)对一个整数的补码再求补码,等于该整数自身。



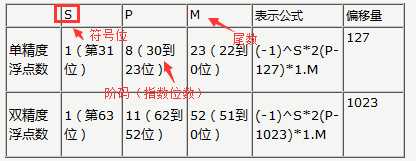
4.为了强制定义一些特殊值,IEEE标准通过指数将表示空间划分成了三大块:
【1】最小值指数(所有位全置0)用于定义0和弱规范数
【2】最大指数(所有位全值1)用于定义±∞和NaN(Not a Number)
【3】其他指数用于表示常规的数。

通常情况,IEEE标准写法,尾数的1,省略,Fraction= 0.001001,因为标准写法,前面 的1总是省略 Fraction = 尾数 - 1 ;(IEEE规定小数点左侧的 1 是隐藏的)
① 第一个域:为符号域。其中 0 表示数值为正数,而 1 则表示负数。
② 第二个域为指数域,对应于我们之前介绍的二进制科学计数法中的指数部分。
指数阈:通常使用移码表示:

注意偏差值的概念:偏差值是为了表示复数引入的值,之前上课讲到的偏差值为128,此文中的偏差值为127
实际的指数值 -127(保存为 全 0),即: 首先-127原码1-111 1111,的补码1-000 0001,然后加上单精度偏执: 0-111 111 ,即结果:0-000 0000,全0. 所以0-000 0000 指数位表示:-127,即e-127
以及 +128(保存为全 1), 即:首先+128原码‘1’-000 0000,的补码, ‘1’-000 0000,然后加上单精度偏执:0-111 111 ,, 即结果:‘1’-111 1111,全1。 即全1 指数位表示:+128,即e+128
这些特殊值,保留用作特殊值的处理。这样,实际可以表达的有效指数范围就在 -127 和 127 之间。在本文中,最小指数和最大指数分别用 emin 和 emax 来表达。
5. 根据IEEE(美国电气和电子工程师学会)754标准要求,无法精确保存的值必须向最接近的可保存的值进行舍入。不过对于二进制浮 点数而言,还多一条规矩,就是当需要舍入的值刚好是一半时,不是简单地进,而是在前后两个等距接近的可保存的值中,取其中最后一位有效数字为零者。
6.据以上分析,IEEE 754标准中定义浮点数的表示范围为:
单精度浮点数 二进制:± (2-2^-23) × 2127 对应十进制: ~ ± 10^38.53
双精度浮点数 二进制:± (2-2^-52) × 21023
7.
(1) 当P=0,M=0时,表示0。
(2) 当P=255,M=0时,表示无穷大,用符号位来确定是正无穷大还是负无穷大。
(3) 当P=255,M≠0时,表示NaN(Not a Number,不是一个数)。
标签:value image 表示法 精度 not nbsp 额外 两种 ber
原文地址:https://www.cnblogs.com/JQbiu/p/10414908.html