标签:扫描法 ext 含义 href image false 通过 hhhh algorithm
写一篇题解,以纪念调了一个小时的经历(就是因为边的数组没有乘2 phhhh QAQ)
题目大意:找一个点使得从这个点出发作为源点,流出的流量最大,输出这个最大的流量。
以这道题来介绍二次扫描和换根法
作为一道不定根的树形DP,如果直接对每个点进行DP,可能时间会炸掉
但是,优秀的二次换根和扫描法可以再O(n^2)内解决问题。
二次扫描的含义:(来自lyd 算法竞赛进阶指南)
第一次扫描:任选一个节点为根节点(我会选1)在树上进行树形DP,在回溯时,从儿子节点向父节点(从底向上)进行状态转移
第二次扫描:从刚才选的根出发,对树进行dfs,在每次递归前进行自顶向下的推导,计算"换根"后的解
在第一次扫描时,我们可以算出以节点u为根的子树中,从u流向其子树的最大流量
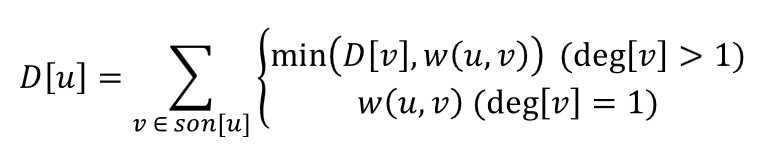
在第二次扫描时,我们通过dfs,可以自上而下的求出以节点u为根,从u流向整个流域(其子树)的最大流量
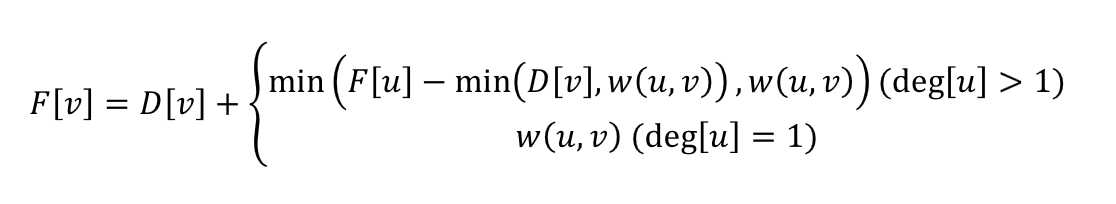
当我们从节点u到节点v时,已经求出F[u],而从u到v的流量为min(D[v],w(u,v)),所以从u流向v的其他部分的流量就是F[u]-min(D[v],w(u,v)),所以拿它再跟w(u,v)取min
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #define R register int using namespace std; const int N=200010; struct edge{ int v,nxt,w; }e[N<<1]; int t,n,ans,cnt; int d[N],f[N],fir[N],deg[N]; bool vis[N]; inline void add(int u,int v,int w) {e[++cnt].v=v,e[cnt].w=w,e[cnt].nxt=fir[u],fir[u]=cnt;} inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch==‘-‘?-1:fix; do ret=(ret<<3)+(ret<<1)+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } void dp(int u) { vis[u]=true,d[u]=0; for(R i=fir[u];i;i=e[i].nxt) { R v=e[i].v; if(vis[v]) continue; dp(v); if(deg[v]==1) d[u]+=e[i].w; else d[u]+=min(d[v],e[i].w); } } void dfs(int u) { vis[u]=true; for(R i=fir[u];i;i=e[i].nxt) { R v=e[i].v; if(vis[v]) continue; if(deg[u]==1) f[v]=d[v]+e[i].w; else f[v]=d[v]+min(f[u]-min(d[v],e[i].w),e[i].w); dfs(v); } } int main() { t=g(); while(t--) { memset(vis,false,sizeof(vis)); memset(fir,0,sizeof(fir)); memset(deg,0,sizeof(deg)); ans=0,cnt=0; n=g(); if(n==0||n==1) {putchar(‘0‘),putchar(‘\n‘);continue;} for(R i=1;i<n;i++) {R u=g(),v=g(),w=g(); add(u,v,w),add(v,u,w); deg[u]++,deg[v]++;} R rt=1; dp(rt); f[rt]=d[rt]; memset(vis,false,sizeof(vis)); dfs(rt); for(R i=1;i<=n;i++) ans=max(ans,f[i]); printf("%d\n",ans); } return 0; }
(我太菜了。。。。QAQ)
题解 poj3585 Accumulation Degree (树形dp)(二次扫描和换根法)
标签:扫描法 ext 含义 href image false 通过 hhhh algorithm
原文地址:https://www.cnblogs.com/Jackpei/p/10420639.html