标签:oid ati 内容 接受 cti htm rate 存在 引入
SVM是支持向量机(Support Vector Machines)的简称,是一种二分类模型。
支持向量机所做的就是去寻找两类数据的分隔线,通常将这个分隔线叫做超平面。
分隔的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。
(1)线性分割
如果一个线性函数能够将样本(比如说两类点)分开,那么称这些数据样本是线性可分的
线性函数在二维空间就是一条直线,在三维空间就是一个平面,在不考虑维数的情况下线性函数统称为超平面。
如图:实心点和空心点是两类点
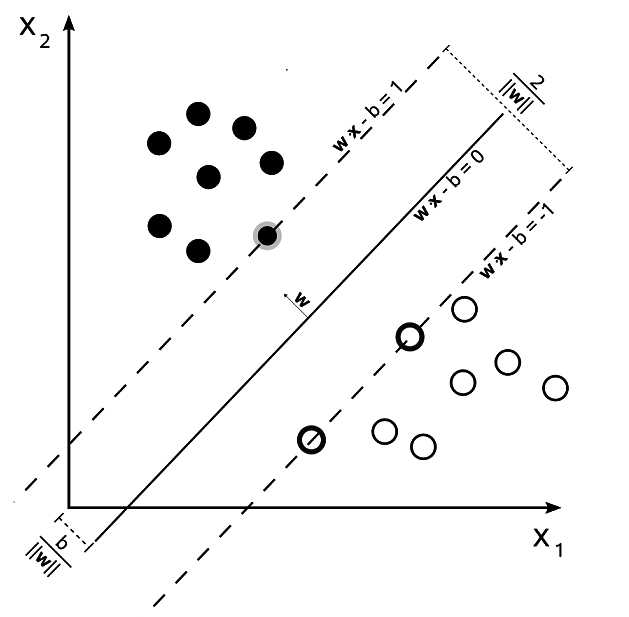
这两类点,有无数条直线可以将它们分隔开
SVM的目标就是在这无数条线中,找出一条线 使这条线与两类样本(两类点)中最近的点距离最大
这个距离叫做 间隔
但有时因为数据的问题不能画出分割线时,例如这样:
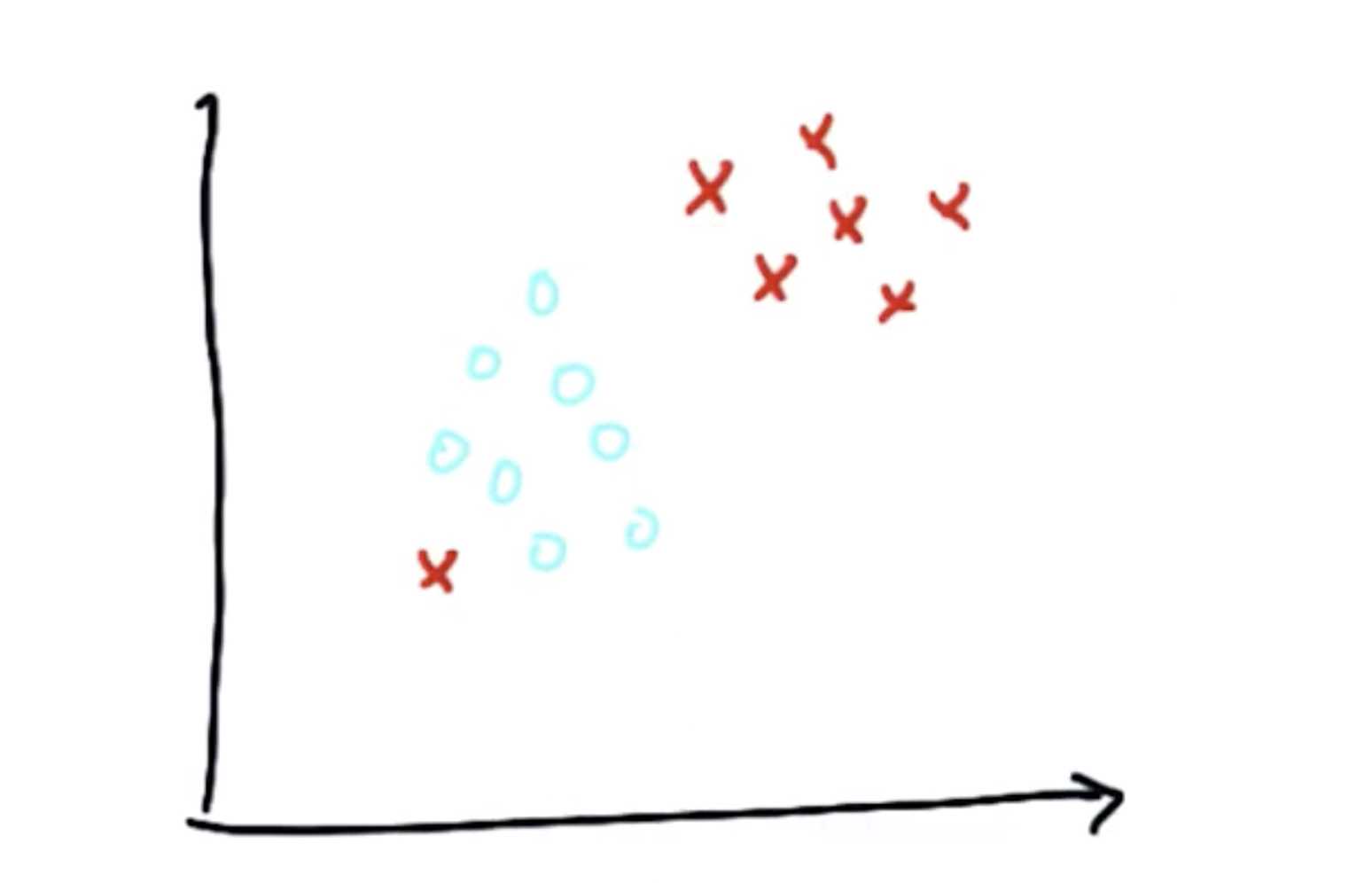
很显然,分隔线是不存在的,这时可以将这个点当作异常来处理
即 忽略这个点,再分割
(2)非线性分割
还有一些数据是用一条直线分割不出来的,就像这样:
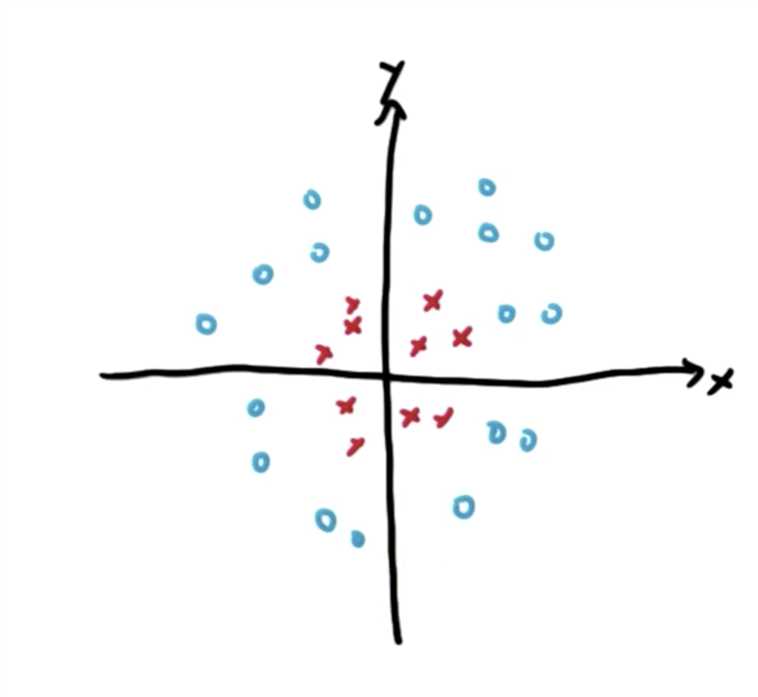
在线性分割时,我们向SVM提供样本的坐标数据(X,Y)即X和Y来进行计算
针对图中的情况,我们可以引入第三个数据Z,令Z = X^2 + Y^2
再画出Z-X图:
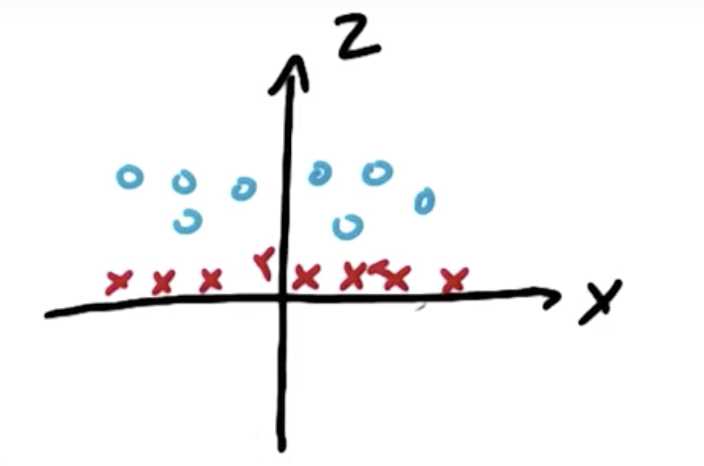
通过这一转化,就可以针对Z,X进行分割
再一个例子
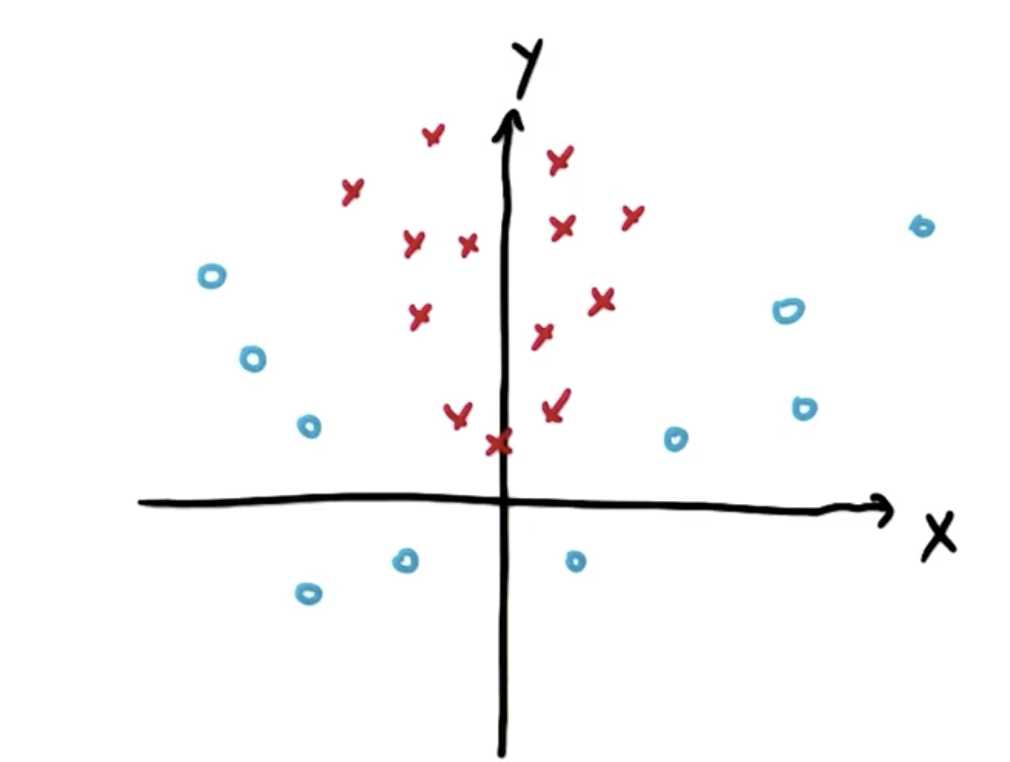
样本无法直接根据X,Y来划分,此时将样本的坐标转化为 |X|,Y 画出图像:
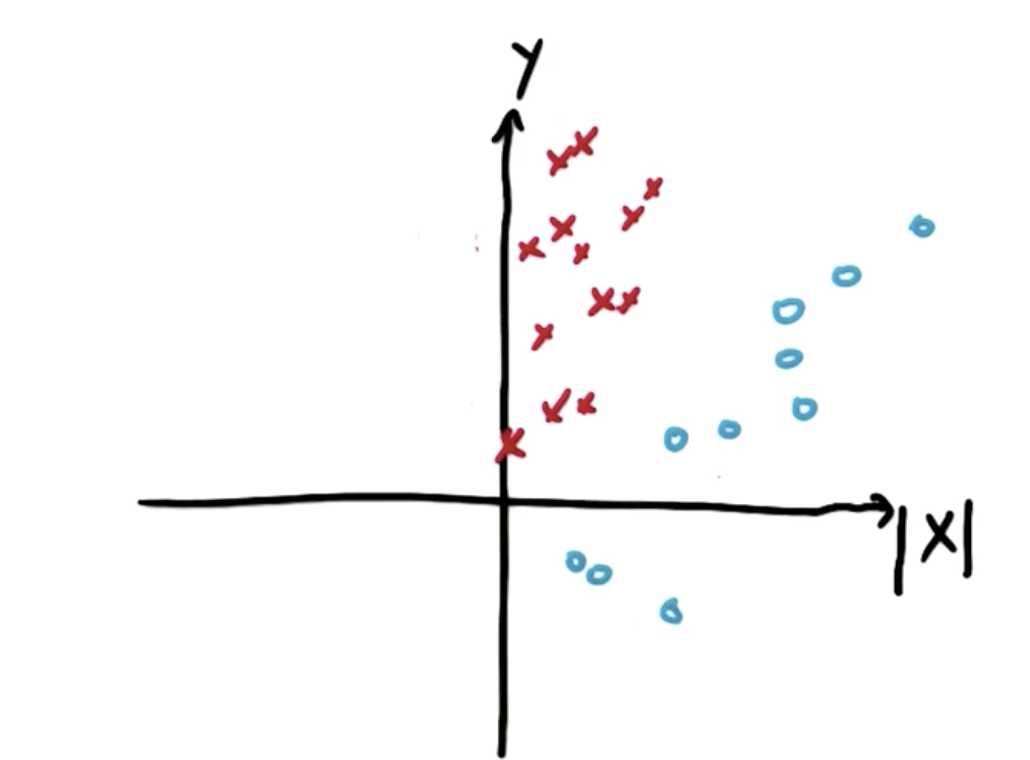
即可划分
(3)核技巧(Kernel Trick)
核函数即是接受低纬度的输入空间或者特征空间,并将其映射到高维度空间,所以过去不可以线性分割的内容变为可分割的。
应用核函数技巧将输入空间从x,y变到更大的输入空间后,再使用支持向量机对数据点进行分类,得到解后返回原始空间
这样就得到了一个非线性分割
核函数有很多种,其中常用的有:
linear(线性),ploy(多项式),rbf(径向基函数),sigmoid(s函数)
在SVM算法中,核函数作为一个参数发挥作用
(4)其他参数(C、gamma)
不仅是核作为参数影响SVM分割,还有其他参数,例如C和Gamma,其中C的影响最大,Gamma几乎没有影响
C的作用:在光滑的决策边界以及尽可能正确分类所有训练点之间进行平衡(C越大正确点越多),但代价时模型更复杂
C=10000,kernal=‘rbf‘ C=10 kernel=‘rbf‘
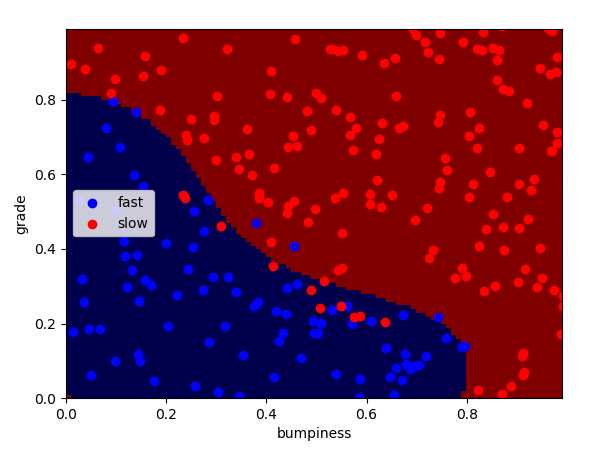
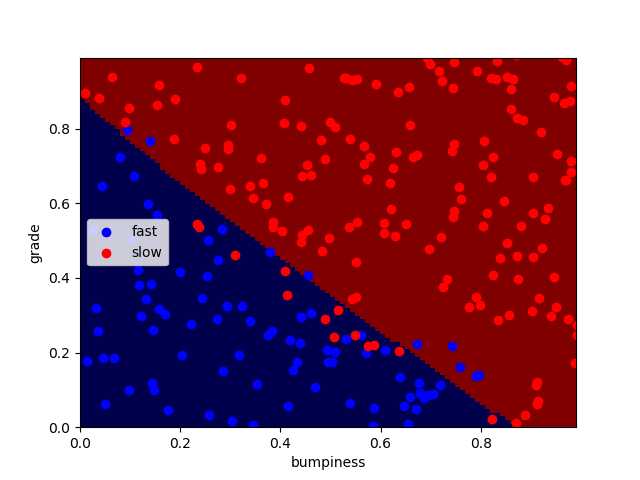
如图 核函数相同时,C相差三个数量级时的区别
通过调整核函数,C和Gamma来避免过拟合现象
环境:MacOS mojave 10.14.3
Python 3.7.0
使用库:scikit-learn 0.19.2
sklearn.SVM库官方文档:https://scikit-learn.org/dev/modules/generated/sklearn.svm.SVC.html
>>> import numpy as np >>> X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])#生成四个训练点 >>> y = np.array([1, 1, 2, 2])#前两个点分为标签1,后两个点分为标签2 >>> from sklearn.svm import SVC >>> clf = SVC(gamma=‘auto‘)#默认核函数线性分割 >>> clf.fit(X, y) #训练 SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape=‘ovr‘, degree=3, gamma=‘auto‘, kernel=‘rbf‘, max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False)#使用rbf核函数,c为1,gamma自动配置 >>> print(clf.predict([[-0.8, -1]])) #预测新的点 [1] #结果为标签1
Main.py 主程序
import sys from class_vis import prettyPicture from prep_terrain_data import makeTerrainData import matplotlib.pyplot as plt import copy import numpy as np import pylab as pl features_train, labels_train, features_test, labels_test = makeTerrainData() ########################## SVM ################################# ### we handle the import statement and SVC creation for you here from sklearn.svm import SVC clf = SVC(kernel="linear",C = 1000) #### now your job is to fit the classifier #### using the training features/labels, and to #### make a set of predictions on the test data clf.fit(features_train, labels_train) #### store your predictions in a list named pred pred = [] pred = clf.predict(features_test) prettyPicture(clf, features_test, labels_test) from sklearn.metrics import accuracy_score acc = accuracy_score(pred, labels_test) print(acc) def submitAccuracy(): return acc
perp_terrain_data.py 生成训练点
#!/usr/bin/python import random def makeTerrainData(n_points=1000): ############################################################################### ### make the toy dataset random.seed(42) grade = [random.random() for ii in range(0,n_points)] bumpy = [random.random() for ii in range(0,n_points)] error = [random.random() for ii in range(0,n_points)] y = [round(grade[ii]*bumpy[ii]+0.3+0.1*error[ii]) for ii in range(0,n_points)] for ii in range(0, len(y)): if grade[ii]>0.8 or bumpy[ii]>0.8: y[ii] = 1.0 ### split into train/test sets X = [[gg, ss] for gg, ss in zip(grade, bumpy)] split = int(0.75*n_points) X_train = X[0:split] X_test = X[split:] y_train = y[0:split] y_test = y[split:] grade_sig = [X_train[ii][0] for ii in range(0, len(X_train)) if y_train[ii]==0] bumpy_sig = [X_train[ii][1] for ii in range(0, len(X_train)) if y_train[ii]==0] grade_bkg = [X_train[ii][0] for ii in range(0, len(X_train)) if y_train[ii]==1] bumpy_bkg = [X_train[ii][1] for ii in range(0, len(X_train)) if y_train[ii]==1] # training_data = {"fast":{"grade":grade_sig, "bumpiness":bumpy_sig} # , "slow":{"grade":grade_bkg, "bumpiness":bumpy_bkg}} grade_sig = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==0] bumpy_sig = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==0] grade_bkg = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==1] bumpy_bkg = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==1] test_data = {"fast":{"grade":grade_sig, "bumpiness":bumpy_sig} , "slow":{"grade":grade_bkg, "bumpiness":bumpy_bkg}} return X_train, y_train, X_test, y_test # return training_data, test_data
class_vis.py 绘图与保存图像
import warnings warnings.filterwarnings("ignore") import matplotlib matplotlib.use(‘agg‘) import matplotlib.pyplot as plt import pylab as pl import numpy as np #import numpy as np #import matplotlib.pyplot as plt #plt.ioff() def prettyPicture(clf, X_test, y_test): x_min = 0.0; x_max = 1.0 y_min = 0.0; y_max = 1.0 # Plot the decision boundary. For that, we will assign a color to each # point in the mesh [x_min, m_max]x[y_min, y_max]. h = .01 # step size in the mesh xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) Z = clf.predict(np.c_[xx.ravel(), yy.ravel()]) # Put the result into a color plot Z = Z.reshape(xx.shape) plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.pcolormesh(xx, yy, Z, cmap=pl.cm.seismic) # Plot also the test points grade_sig = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==0] bumpy_sig = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==0] grade_bkg = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==1] bumpy_bkg = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==1] plt.scatter(grade_sig, bumpy_sig, color = "b", label="fast") plt.scatter(grade_bkg, bumpy_bkg, color = "r", label="slow") plt.legend() plt.xlabel("bumpiness") plt.ylabel("grade") plt.savefig("test.png")
得到结果:正确率92%
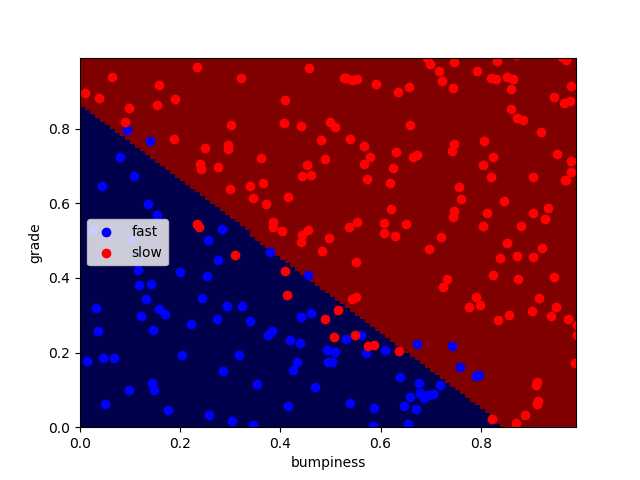
在数据点不变的情况下,使用rbf核,并使C的值设定为1000,10000,100000
clf = SVC(kernel="rbf",C = 100000)
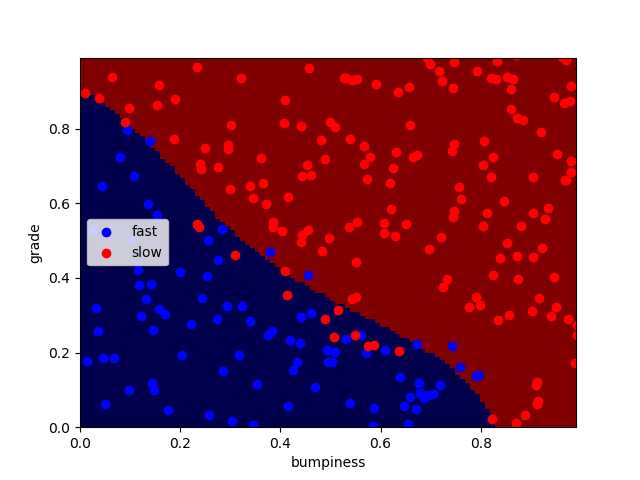
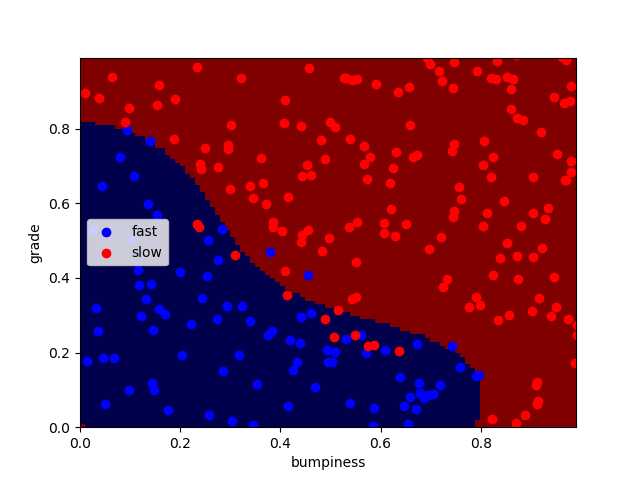
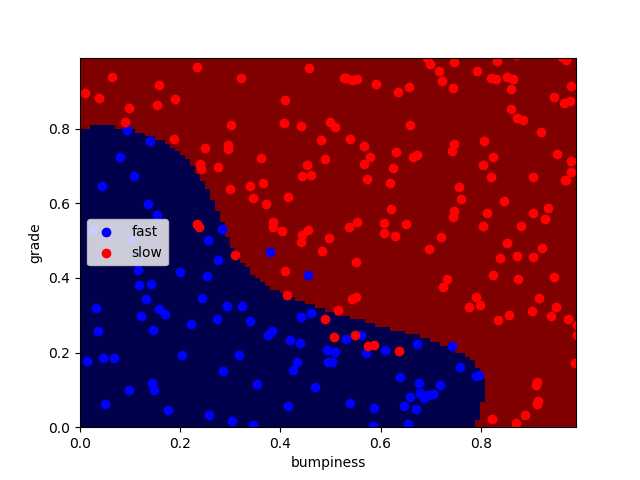
正确率分别为:92.4% 93.2% 94.4%
同时编译时间略微变长
有时训练集过大会使训练时间非常长,此时我们可以通过缩小训练集的方式来加快训练速度。
在训练分类器前加上这两句代码,可使训练集变为原本的1%:
features_train = features_train[:len(features_train)/100]
labels_train = labels_train[:len(labels_train)/100]
支持向量机在具有复杂领域和明显分割边界的情况下,表现十分出色。
但是,在海量数据集中,他的表现不太好,因为在这种规模的数据集中,训练时间将是立方数。(速度慢)
另外,在噪音过多的情况下,效果也不太好。(可能会导致过拟合)
标签:oid ati 内容 接受 cti htm rate 存在 引入
原文地址:https://www.cnblogs.com/Joeric07/p/10425174.html