AC自动机初步

标签：href   mic   for   表示   基础上   应该   数组   logs   状态   

概述

应用场景：多模字符串匹配问题。

KMP解决的问题是两个字符串之间的互相匹配，而如果有多个字符串要和一个字符串进行匹配呢？如果还用KMP的话，复杂度依然上天，所以，一个正常的想法是在KMP的基础上堆数据结构。

所以AC自动机=在Trie树上跑KMP，它其中也存在失配数组，与KMP类似。

初见

AC自动机的基础是Trie树。和Trie树不同的是，树中的每个结点除了有指向孩子的指针（或者说引用），还有一个fail指针，它表示输入的字符与当前结点的**所有孩子结点都不匹配时**(注意，不是和该结点本身不匹配)，自动机的状态应转移到的状态（或者说应该转移到的结点）。fail指针的功能可以类比于KMP算法中next数组的功能。

我们现在来看一个用目标字符串集合{abd,abdk, abchijn, chnit, ijabdf, ijaij}构造出来的AC自动机

-----By nullzx

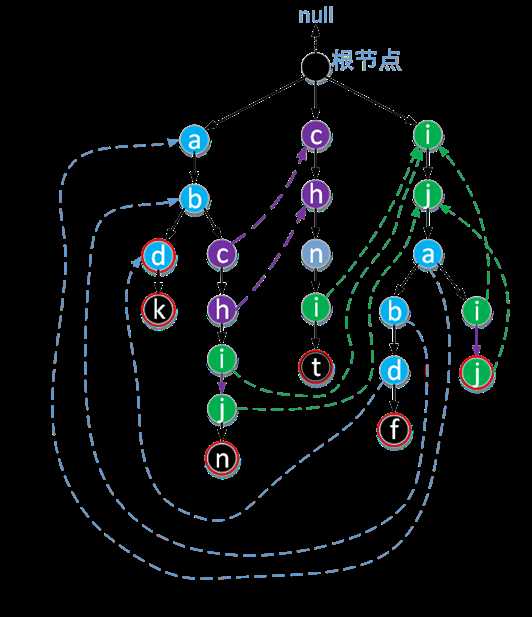
也就是说，f函数所指向的点，与当前点之间有最长后缀。

每个结点的fail指针表示由根结点到该结点所组成的字符序列的所有后缀　和　整个目标字符串集合（也就是整个Trie树）中的所有前缀 两者中最长公共的部分。 by nullzx

这里与KMP却有异曲同工之妙。

应用

假设已经处理出了f函数，那么该如何应用呢？

我们知道\(f[]\)表示的是当前点的最长后缀，那么，AC自动机的运行就要进行以下步骤（设cur为Trie树中的光标）：

1. 要匹配的字符串光标往后移一位
2. 检测\(cur\)的后继状态中是否存在合法情况（\(pa[cur][S[i]-'a']?\)）。
3. 如果存在，则将所有的包含该后缀的点的后缀都统计一遍。

for(int i=0,j=0;i<l;i++){
    j=pa[j][S[i]-'a'];
    for(int k=j;k;k=f[k])
        if(val[k])ans+=val[k],val[k]=0; 
}

还是要具体例子具体分析，应用三言两语是讲不清楚的。

fail数组

重点还是在这个fail数组的处理上。

先上代码：

void get_fail(){
    queue<int>Q;
    for(int i=0;i<26;i++){
        if(pa[0][i]!=0){
            f[pa[0][i]]=0;
            Q.push(pa[0][i]);   
        }
    }
    while(!Q.empty()){
        int u=Q.front();Q.pop();
        for(int i=0;i<26;i++){
            if(pa[u][i]!=0){
                f[pa[u][i]]=pa[f[u]][i];
                Q.push(pa[u][i]);
            }
            else pa[u][i]=pa[f[u]][i];
        }
    }
}

其实这就是板子，对照上面的图，多模拟几下应该很好理解。。。（太懒了，我受不了了。。。）

AC自动机初步

标签：href   mic   for   表示   基础上   应该   数组   logs   状态   

原文地址：https://www.cnblogs.com/zryabc/p/10427896.html