标签:水平 hat too 机器学习 利用 技术 阅读 获得 失败
目录
近期广泛阅读券商关于宏观高频数据的研报,发现了两点不足:
- 就研究手段而言,比较粗放,普遍停留在仅仅比较数据相关系数的层面;
- 就理论高度而言,很少探讨数据背后的因果关联。
不过有些理念先进的券商团队已经开始从产业链传导的角度试图细致的描述数据间的关联,这正好契合了下面这篇文章的核心概念——有向无环图(DAG)。
本文翻译自《"Correlation is not causation". So what is?》
链接:https://iyarlin.github.io/2019/02/08/correlation-is-not-causation-so-what-is/
在过去几年中,机器学习应用的数量和范围都在迅速增长。什么是因果推断,它与传统的 ML 有什么不同?什么时候应该考虑使用它?在本报告中,我尝试通过一个例子给出一个简短而具体的答案。
想象一下,营销团队的任务是找到提高营销支出对销售的影响。我们拥有营销支出(mkt)、网站访问(visits)、销售(sales)和竞争指数(comp)的记录。
我们将使用一组方程(也称为结构方程)来模拟数据集:
\[ sales = \beta_1vists + \beta_2comp + \epsilon_1 \vists = \beta_3mkt + \epsilon_2\mkt = \beta_4comp + \epsilon_3\comp = \epsilon_4 \]
其中 \(\{\beta_1, \beta_2, \beta_3\, \beta_4\} = \{0.3, -0.9, 0.5, 0.6\}\).
下面图片中展示以及拟合模型用到的所有数据均由上面的等式模拟得到。
以下是数据集的前几行:
| mkt | visits | sales | comp |
|---|---|---|---|
| 282.5 | 2977 | 379 | 3.635 |
| 338.8 | 3149 | 308 | 4.515 |
| 303.9 | 2485 | 369 | 3.092 |
| 558.8 | 3117 | 191 | 5.22 |
| 334.4 | 4038 | 286 | 4.281 |
| 297.7 | 2854 | 441 | 3.592 |
我们的目标是,得到预测营销支出对销售额的影响是 0.15 的结论(根据上面的方程组,对分项目做乘积,我们得到 \(\beta_1 \cdot \beta_3 = 0.3 \cdot 0.5 = 0.15\))。
我们通常从画出 sales 和 mkt 之间的散点图开始:
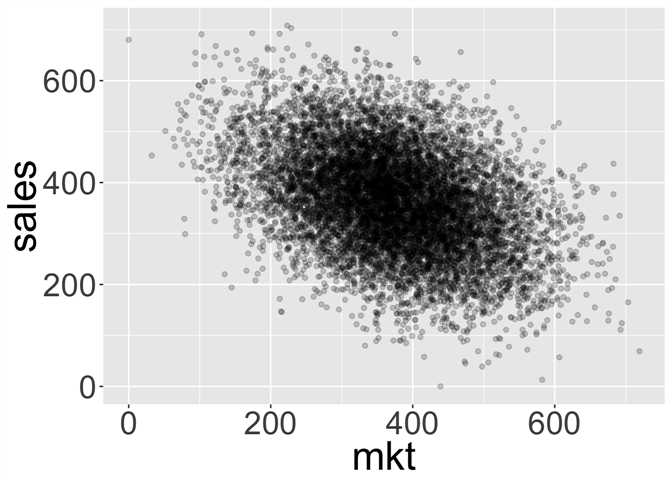
我们可以看到图中看到的关系实际上与我们预期的相反!看起来增加营销实际上会降低销售额。实际上,不仅相关性不是因果关系,有时它可能表现出与真实因果关系相反的关系。
拟合一个简单的线性模型 \(sales = r_0 + r_1mkt + \epsilon\) 将会产生下面的系数:(注意,\(r\) 泛指回归系数,而 \(\beta\) 泛指结构方程中真实的参数)
| (Intercept) | mkt |
|---|---|
| 513.5 | -0.3976 |
确认我们得到的效果与我们想要的效果截然不同(0.15)。
有人可能会假设,查看双变量关系相当于仅使用 1 个预测变量,但如果我们要使用所有可用的特征,我们可能能够找到更准确的估计。
运行回归模型 \(sales = r_0 + r_1mkt + r_2visits + r_3comp + \epsilon\),得到下面的系数:
| (Intercept) | mkt | visits | comp |
|---|---|---|---|
| 596.7 | 0.009642 | 0.02849 | -90.06 |
现在看来营销支出几乎没有任何影响!我们从线性方程模拟数据,并且我们知道即使使用更复杂的模型(例如 XGBoost、GAM)也无法产生更好的结果(我建议有疑虑的读者通过重新运行 Rmd 脚本来尝试一下生成报告)。
到目前为止我们获得的结果相当令人困惑,我们进而咨询营销团队,我们了解到,在竞争激烈的市场中,团队通常会增加营销支出(这反映在系数 \(\beta_4 = 0.6\) 以上)。因此,竞争可能是一个“混杂”因子:当我们观察到高营销支出时,竞争也会很激烈,从而导致销售额下降。
此外,我们注意到营销可能会影响网站的访问,而这些访问又会影响销售。
我们可以使用有向无环图(DAG)可视化这些特征的相互依赖性:
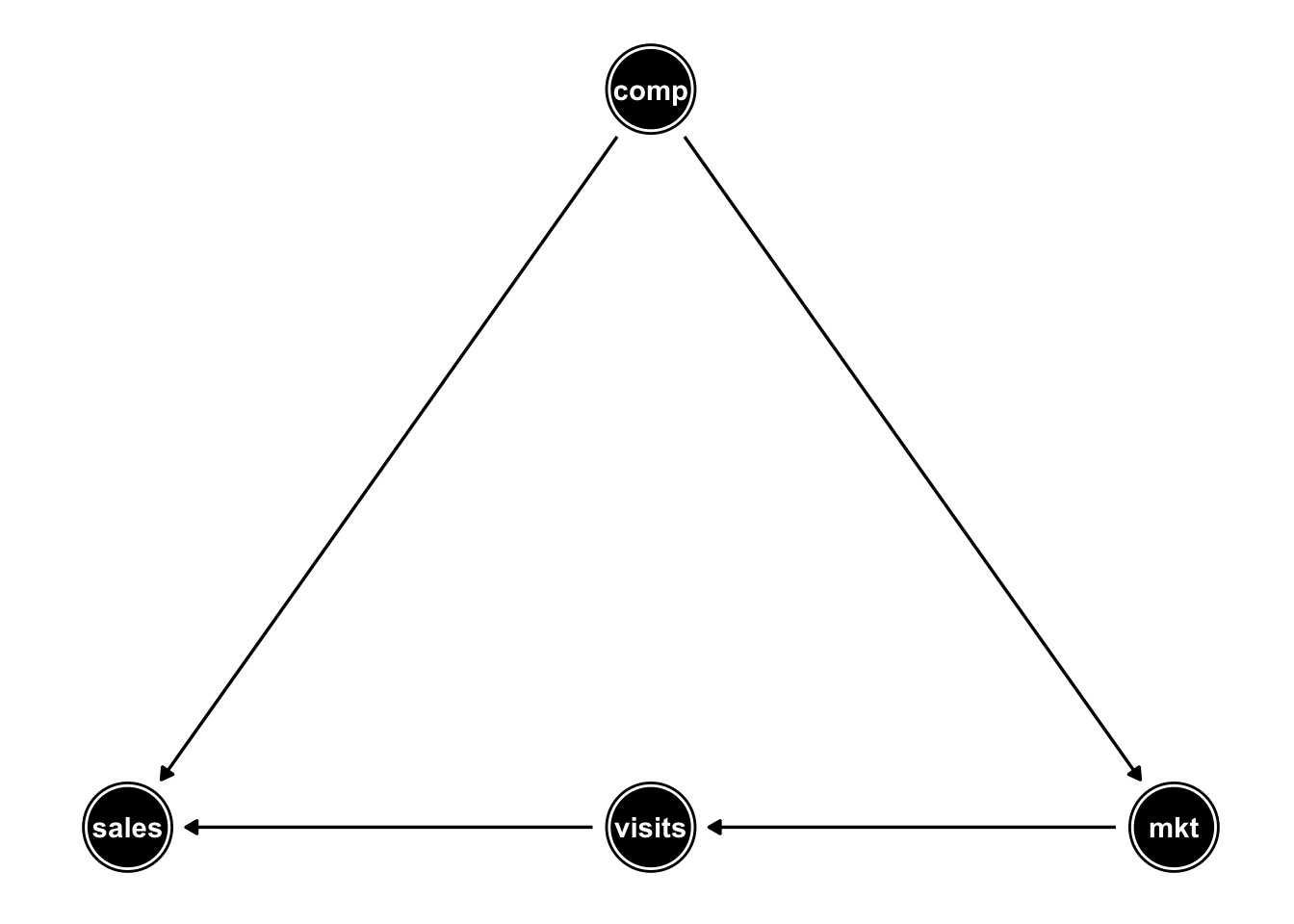
因此,通过将混杂竞争加到我们的回归是有意义的。而在我们的模型中添加访问可能会“屏蔽”或“消解”营销对销售的影响,所以我们应该从我们的模型中省略它。
运行回归模型 \(sales = r_0 + r_1mkt + r_2comp + \epsilon\),得到下面的系数:
| (Intercept) | mkt | comp |
|---|---|---|
| 654.8 | 0.1494 | -89.8 |
现在我们终于得到了正确的效果估计!
我们解决问题的方式有点不稳健。我们提出了诸如特征的“混杂”和“屏蔽”等一般概念。试图将这些应用于由数十个具有复杂关系的变量组成的数据集可能会非常困难。
到目前为止,我们已经看到,试图通过检查双变量图来估计营销支出对销售的影响可能会失败。我们还看到,将所有可用特征抛入我们的标准 ML 模型也会失败。看起来我们需要仔细构建模型中包含的协变量集,以获得真实的效果。
在因果推断中,该协变量集合也称为“调整集”。给定模型的 DAG,我们可以利用各种算法,这些算法非常类似于上面提到的规则,例如“混杂”和“屏蔽”,以找到正确的调整集。
可以获得正确调整集的最基本算法之一是由 J. Pearl 开发的“Backdoor-criteria”。简而言之,它寻求调整集,屏蔽“暴露”变量(例如营销)和“结果”变量(例如销售)之间的每一个“虚假”路径,同时保持影响路径存在。
考虑下面的 DAG,我们试图找到 x5 对 x10 的影响:
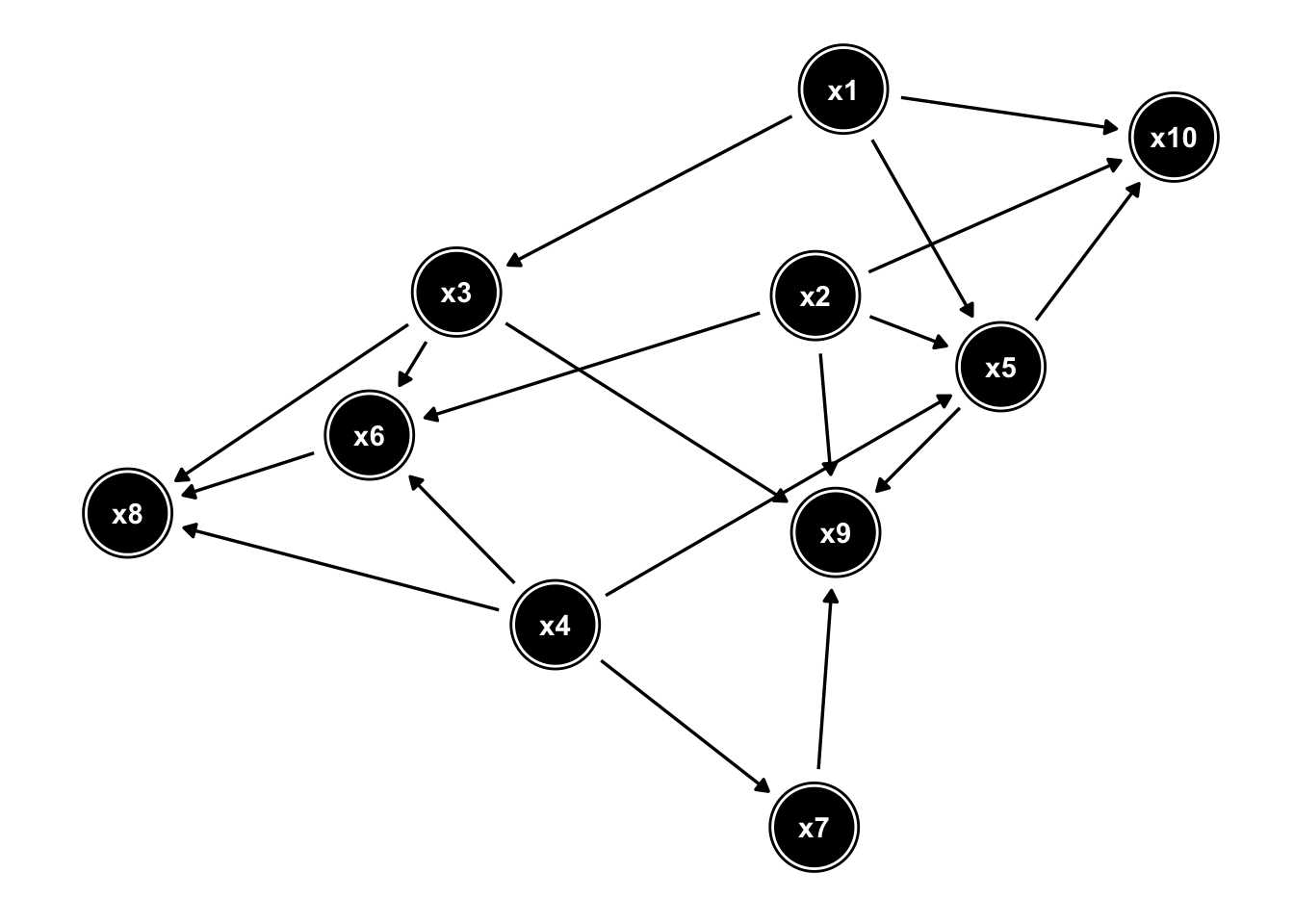
使用 backdoor-criterion 算法(由 R 包 dagitty 实现),我们找到正确的调整集:
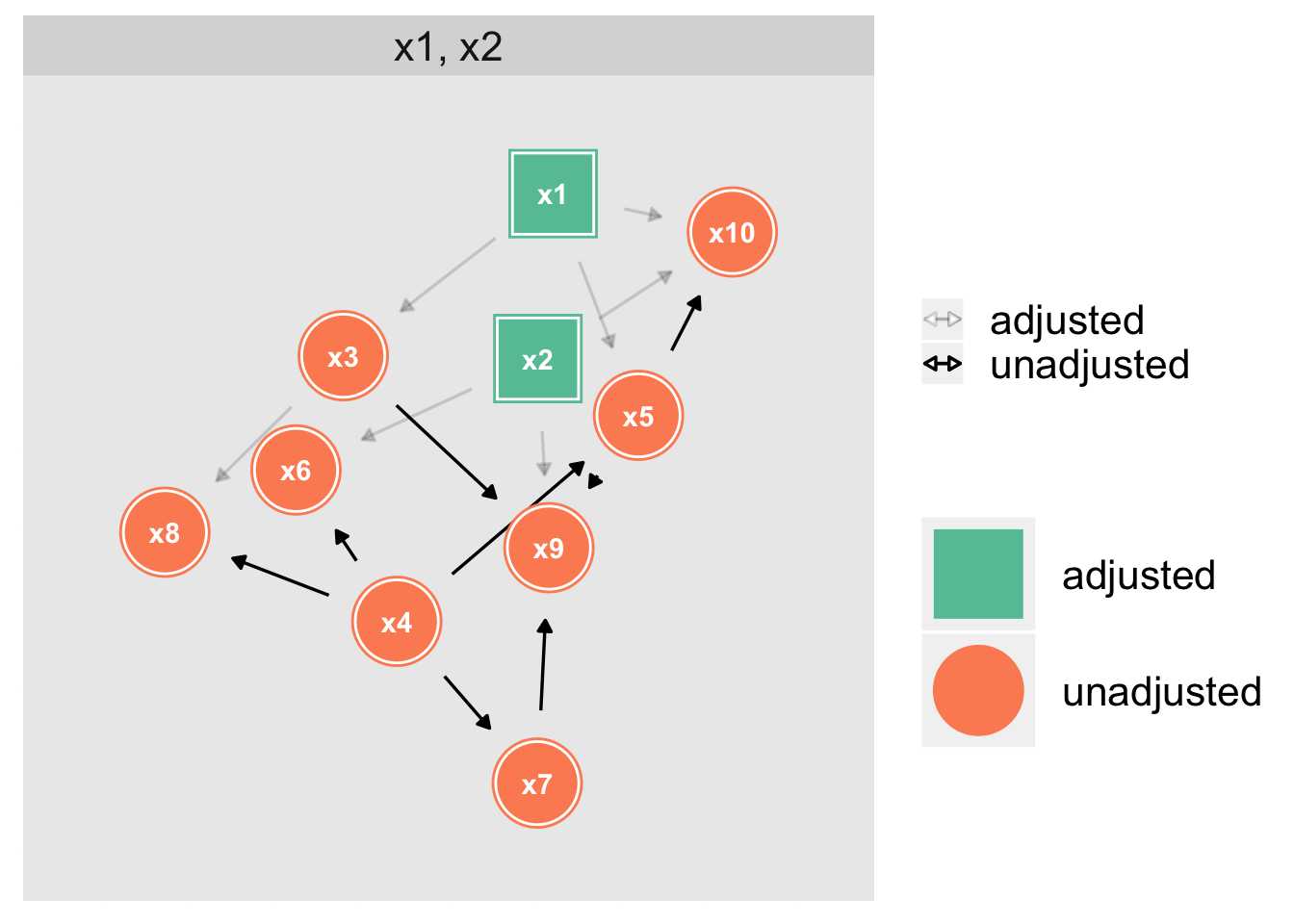
诚然,找到模型的 DAG 非常有挑战性。可以综合考虑下列几种方法:
mgm 或 bnlearn)我会在后面的文章中展开这些主题。
想要进一步了解上述问题的朋友,我推荐阅读 Pearl 写的一篇轻量级的技术报告——《The Seven Tools of Causal Inference with Reflections on Machine Learning》。
想要深入了解因果推断与 DAG 机制的话,我推荐 Pearl 的小册子——《Causal Inference in Statistics - A Primer》。
标签:水平 hat too 机器学习 利用 技术 阅读 获得 失败
原文地址:https://www.cnblogs.com/xuruilong100/p/10434564.html