POI2011 棒棒糖 Lollipop

标签：scanf   span   pop   构造   name   题解   ref   ipo   去掉   

POI2011 棒棒糖 Lollipop

题目传送门

题意

\(Byteasar\)在比特镇开了一家糖果店，草莓香草味的棒棒糖是当地孩子们的最爱。这些棒棒糖都是由长度相同的香草味或者草莓味的片段组成的。一整根棒棒糖的价格是每一段棒棒糖的价格之和，每一段香草味的棒棒糖价格为一元，草莓味的棒棒糖价格为两元。

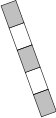
图1：举个例子，这是一根由五段组成的棒棒糖，草莓味和香草味的棒棒糖交替排列，这根棒棒糖的价格为\(8\)元。

现在，\(Byteasar\) 只剩下最后一根棒棒糖了。这根棒棒糖太长了，因此 \(Byteasar\) 认为绝对没有人会买下这一整根。所以，他想要把这一整根在接缝处掰成几段，每一段单独出售。

\(Byteasar\) 的人生经验告诉他，他的顾客希望把自己的钱花在单独的一根棒棒糖上，于是他想知道这一根棒棒糖有没有连续的一段的价格是 \(k\)。但这个问题对他来说太难了，他希望你能帮帮他。

题解

考虑如何构造，假设当前考虑到了第\(i\)位，前\(i-1\)位的价值和为\(sum\)，如果第\(i\)为价值为\(1\)，那么很显然可以直接构造出\(sum+1\)，如果价值为\(2\)，那么我们只能够直接构造出\(sum+2\)，接下来考虑如何构造\(sum+1\)。我们记\(ct_i\)表示从第\(i\)为开始有多少连续的\(2\)，那么我们比较\(ct_1\)和\(ct_i\)。如果\(ct_1<ct_i\)，那么我们可以去掉前\(ct_1\)个\(2\)，加上\(i\)之后\(ct_i\)个\(2\)，这样一段的和仍然是\(sum\)，然后再加上\(1+ct_1+1\)这一位上的1，这样一段的和就是\(sum+1\)，\(ct_1>=ct_i\)也是类似，如此\(O(n)\)构造即可。

Code

#include<bits/stdc++.h>
using namespace std;
const int N=4e6+500;
int n,m,sum;
char s[N];
int l[N],r[N],ct[N];

int main() {
  scanf("%d%d",&n,&m);
  scanf("%s",s+1);
  for(int i=n;i;i--) {
    if(s[i]=='T') ct[i]=ct[i+1]+1;
    else ct[i]=0;
  }
  for(int i=1;i<=n;i++) {
    sum+=s[i]=='T'?2:1;
    l[sum]=1;r[sum]=i;
    if(s[i]=='T') {
      if(ct[1]<ct[i]) l[sum-1]=2+ct[1],r[sum-1]=i+ct[1];
      else l[sum-1]=1+ct[i],r[sum-1]=i+ct[i];
    }
  }
  for(int i=1,k;i<=m;i++) {
    scanf("%d",&k);
    if(l[k]>=1&&r[k]<=n) printf("%d %d\n",l[k],r[k]);
    else puts("NIE");
  }
  return 0;
}

POI2011 棒棒糖 Lollipop

标签：scanf   span   pop   构造   name   题解   ref   ipo   去掉   

原文地址：https://www.cnblogs.com/Apocrypha/p/10445935.html