标签:define unsigned gcd line div 问题 技术 names ref
设g(i,j)表示前i个小朋友分j个糖果的权值乘积和
很容易得到一个式子
这个显然是一个卷积用FFT就可以处理
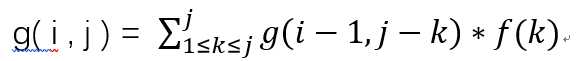
但是问题来了 我们如何得到ans呢
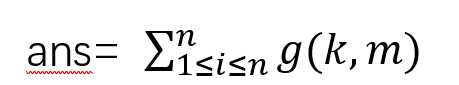
n<=1e8 朴素的算法不太行
要想办法优化一下
然后我就被卡死了 去看了网上的各种题解
顺便拔下来了一个封装性很好的FFT板子
然后你就看的懂下面这个式子了

然后就可以套快速幂了

1 #include <cstdio> 2 #include <cstring> 3 #include <queue> 4 #include <cmath> 5 #include <algorithm> 6 #include <set> 7 #include <iostream> 8 #include <map> 9 #include <stack> 10 #include <string> 11 #include <vector> 12 #define eps 1e-9 13 #define fi first 14 #define se second 15 #define rtl rt<<1 16 #define rtr rt<<1|1 17 #define bug printf("******\n") 18 #define mem(a,b) memset(a,b,sizeof(a)) 19 #define name2str(x) #x 20 #define fuck(x) cout<<#x" = "<<x<<endl 21 #define f(a) a*a 22 #define sf(n) scanf("%d", &n) 23 #define sff(a,b) scanf("%d %d", &a, &b) 24 #define sfff(a,b,c) scanf("%d %d %d", &a, &b, &c) 25 #define sffff(a,b,c,d) scanf("%d %d %d %d", &a, &b, &c, &d) 26 #define pf printf 27 #define FRE(i,a,b) for(i = a; i <= b; i++) 28 #define FREE(i,a,b) for(i = a; i >= b; i--) 29 #define FRL(i,a,b) for(i = a; i < b; i++)+ 30 #define FRLL(i,a,b) for(i = a; i > b; i--) 31 #define FIN freopen("data.txt","r",stdin) 32 #define gcd(a,b) __gcd(a,b) 33 #define lowbit(x) x&-x 34 #define rep(i,a,b) for(int i=a;i<b;++i) 35 #define per(i,a,b) for(int i=a-1;i>=b;--i) 36 using namespace std; 37 typedef long long LL; 38 typedef unsigned long long ULL; 39 int modu; 40 namespace FFT { 41 const double pi = acos ( -1.0 ); 42 struct cpx { 43 double a, b; 44 cpx ( double a = 0, double b = 0 ) : a ( a ), b ( b ) {} 45 inline void init() { 46 a = 0, b = 0; 47 } 48 inline cpx operator + ( const cpx &ano ) const { 49 return cpx ( a + ano.a, b + ano.b ); 50 } 51 inline cpx operator - ( const cpx &ano ) const { 52 return cpx ( a - ano.a, b - ano.b ); 53 } 54 inline cpx operator * ( const cpx &ano ) const { 55 return cpx ( a * ano.a - b * ano.b, b * ano.a + a * ano.b ); 56 } 57 }; 58 typedef cpx C; 59 typedef vector<C> vc; 60 typedef vector<int> vi; 61 62 vc a, b; 63 64 void DFT ( vc &a, int oper = 1 ) { 65 int n = a.size(); 66 for ( int i = 0, j = 0; i < n; ++i ) { 67 if ( i > j ) swap ( a[i], a[j] ); 68 for ( int l = n >> 1; ( j ^= l ) < l; l >>= 1 ); 69 } 70 for ( int l = 1, ll = 2; l < n; l <<= 1, ll <<= 1 ) { 71 double x = oper * pi / l; 72 C omega = 1, omegan ( cos ( x ), sin ( x ) ); 73 for ( int k = 0; k < l; ++k, omega = omega * omegan ) { 74 for ( int st = k; st < n; st += ll ) { 75 C tmp = omega * a[st + l]; 76 a[st + l] = a[st] - tmp; 77 a[st] = a[st] + tmp; 78 } 79 } 80 } 81 if ( oper == -1 ) for ( int i = 0; i < n; ++i ) a[i].a /= n; 82 } 83 84 vi& operator * ( const vi &v1, const vi &v2 ) { 85 int s = 1, ss = ( int ) v1.size() + ( int ) v2.size(); 86 while ( s < ss ) s <<= 1; 87 a.resize ( s ), b.resize ( s ); 88 for ( int i = 0; i < s; ++i ) a[i].init(), b[i].init(); 89 for ( int i = 0; i < v1.size(); ++i ) a[i] = v1[i]; 90 for ( int i = 0; i < v2.size(); ++i ) b[i] = v2[i]; 91 DFT ( a ), DFT ( b ); 92 for ( int i = 0; i < s; ++i ) a[i] = a[i] * b[i]; 93 DFT ( a, -1 ); 94 static vi res; 95 res.resize ( v1.size() ); 96 for ( int i = 0; i < v1.size(); ++i ) res[i] = ( a[i].a + 0.5 ), res[i] %= modu ; 97 return res; 98 } 99 100 void operator *= ( vi &v1, const vi &v2 ) { 101 int s = 1, ss = ( int ) v1.size() + ( int ) v2.size(); 102 while ( s < ss ) s <<= 1; 103 a.resize ( s ), b.resize ( s ); 104 for ( int i = 0; i < s; ++i ) a[i].init(), b[i].init(); 105 for ( int i = 0; i < v1.size(); ++i ) a[i] = v1[i]; 106 for ( int i = 0; i < v2.size(); ++i ) b[i] = v2[i]; 107 DFT ( a ), DFT ( b ); 108 for ( int i = 0; i < s; ++i ) a[i] = a[i] * b[i]; 109 DFT ( a, -1 ); 110 for ( int i = 0; i < v1.size(); ++i ) v1[i] = ( a[i].a + 0.5 ), v1[i] %= modu ; 111 } 112 113 void operator += ( vi &v1, const vi &v2 ) { 114 for ( int i = 0; i < v1.size(); ++i ) v1[i] = ( v1[i] + v2[i] + modu ) % modu; 115 } 116 } 117 118 using namespace FFT; 119 int m, p, n, o, s, u; 120 vi f; 121 vi expmod ( const vi&v, int b ) { 122 vi res ( v.size(), 0 ), tmp = v; 123 res[0] = 1; 124 while ( b ) { 125 if ( b & 1 ) res *= tmp; 126 tmp *= tmp; 127 b = b >> 1; 128 } 129 return res; 130 } 131 vi& solve ( int n ) { 132 static vi res, ghalf; 133 if ( n == 1 ) return res = ghalf = f; 134 solve ( n / 2 ); 135 res += res * ghalf; 136 ghalf *= ghalf; 137 if ( n & 1 ) res += expmod ( f, n ), ghalf *= f; 138 return res; 139 } 140 int main() { 141 //FIN; 142 sff ( m, modu ); 143 sffff ( n, o, s, u ); 144 f = vi ( m + 1, 0 ); 145 for ( int i = 1 ; i < m + 1 ; i++ ) f[i] = ( 1LL * o * i * i + s * i + u ) % modu; 146 vi &res = solve ( min ( n, m ) ); 147 printf ( "%d\n", res[m] ); 148 return 0; 149 }
bzoj 4332 FFT型的快速幂(需要强有力的推导公式能力)
标签:define unsigned gcd line div 问题 技术 names ref
原文地址:https://www.cnblogs.com/qldabiaoge/p/10447097.html