标签：适合 总数 col 假设 缓解 偏差 深度学习 img val
一.经验误差和过拟合
错误率 E=a/m, a分类错误的样本数，m样本总数
精度 = 1 - E。
学习器在训练集上的误差：训练误差；在新样本上的误差：泛化误差。好的学习器应在新样本上表现优秀，因此学习器应尽可能掌握样本的潜在规律，提升泛化性能。
过拟合：学习能力过于强大，样本训练时将样本“自身特点”当做潜在样本的“一般规律”，导致泛化能力下降。
欠拟合：学习能力低下，对训练样本的一般性质未掌握好。
一般来说，欠拟合比较容易克服，如决策树-增加分支，神经网络-增加训练轮数等。而过拟合是机器学习的关键障碍，在机器学习算法中过拟合是无法避免的，应尽可能缓解或是减小其风险。
二.模型选择-评估方法
对于model selection问题，由于无法直接根据泛化误差进行评估，而训练误差由于过拟合的存在不适合作为评估标准。通常选用试验测试的方法得到“测试误差”作为近似的泛化误差。测试集应尽量与训练集互斥。
对于只有一个包含m个样例的数据集D={(x1,y1), (x2,y2), ...., (xm,ym)}。通常对D进行适当处理产生训练集S和测试集T。
1.留出法
D = S U T，S、T互斥
将D直接划分为互斥的两个集合作为S和T，并保持S、T的样本类别比例和D相似（即分层采样）。由于样本个体差异性，划分方式有很多种，在使用留出法时一般做若干次随机划分、重复进行实验评估后取平均值作为评估结果。常见做法将2/3~4/5的样本用于训练，其余用于测试。
缺点：若训练集S包含绝大多数样本，S训练模型可能更接近用D训练模型，测试集T较小，评估结果不够稳定准确（方差较大）
若测试机T较大，则S训练模型与D训练模型可能有较大差别，降低评估结果的保真性（偏差较大）。
2.交叉验证法（k折交叉验证 k-fold cross validation）
D = D1 U D2 U ... U Dk，Di和Dj互斥（i != j）
将D划分为k(常用k=10)个互斥的子集D1~Dk，每个子集对D分层采样得到。每次用k-1个子集作为训练集，剩下一个作为测试集，进行k次训练和测试，最终返回均值。同留出法类似，通常随机使用不同的划分重复p次，即p次k折交叉验证法，最终返回均值。
留一法：假设D包含m个样本，令k=m，将m个样本划分为m个子集采用k折交叉验证。导致绝大多数情况下S训练模型与D训练模型很相似，计算复杂度高，适用于数据集不是很大的情况。
3.自助法（bootstrapping）
对包含m个样本的数据集D进行m次随机采样生成D‘作为训练集，而集合(D - D‘)作为测试集。对自助法分析如下：
易得样本在m次采样中均不被采用的概率为
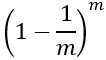，对m取极限得到
。
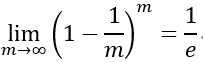通过自助采样，大约有1/e(36.8%)的样本未出现在训练集中。这样，实际模型和期望模型都采用m个训练样本，同时仍有总数据大约1/3的样本可以用于测试，这样的测试结果称为“包外估计”。自助法大多用于训练集较小、难以有效分类的数据集，对集成学习有很大好处。
缺点：bootstrapping改变了初始数据集的分布，会引入估计偏差。若初始数据量足够，留出法和交叉验证法更常用一些。
4.算法调参(parameter tuning)
大多数学习算法都有参数设定，参数配置不同学得的模型性能往往不同。因此，对适用学习算法不仅要进行选择，还需对算法参数进行配置。
一个有效的学习算法往往有庞大规模的参数设置。在机器学习中，参数涉及两类：
超参数：即算法的参数。
模型参数：对于大型深度学习算法往往有巨量的调参工作。
两者的调参方式类似，都是产生多种模型后基于某种评估算法进行评估。不同之处在于超参数通常由人工设定调参，模型参数则通过学习产生多个候选模型（如神经网络在不同轮数停止训练）。
标签：适合 总数 col 假设 缓解 偏差 深度学习 img val
原文地址：https://www.cnblogs.com/KrianJ/p/10465672.html
