链式法则玩转反向传播

标签：直接   传递   ror   nbsp   com   理解   逻辑回归   跳过   蓝色   

神经网络的反向传播到底是个什么样的过程？今天就用链式求导揭开这个黑盒子。

这对于理解和设计神经网络很有帮助。

我们使用一个简单的逻辑回归的例子

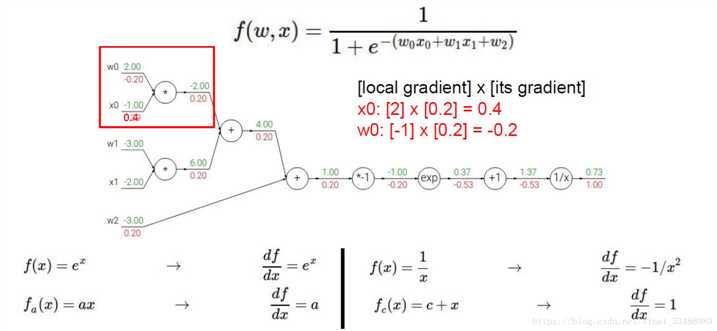
这里绿色是前向计算，褐红色是反向传播。 0.73是最终输出，1是误差。

可以看到整个计算流程就是上面那个逻辑回归表达式。

好了，误差有了，开始反向传播吧

很简单，就是拿误差乘以导数

error=1，它是经过1/x计算得到的误差，导数f1=-1/x^2，反向传递 　　1X(-1/1.37^2)=-0.53

error=-0.53，它是经过x+1计算得到的误差，导数f2=1，反向传递　　  -0.53X(1)=f1Xf2=-0.53

error=-0.53，它是经过e^x计算得到的误差，导数f3=e^x，反向传递　　   -0.53X(e^-1)=f1Xf2Xf3=-0.2

error=-0.2，它是经过-x计算得到的误差，导数f4=-1，反向传递　　      -0.2X(-1)=f1Xf2Xf3Xf4=0.2

error=0.2，它是经过m1+m2计算得到的误差，它有2个导数，

　　　　　　　　　　　　　　  对m1的导数f51=1，反向传递　　      0.2X(1)=f1Xf2Xf3Xf4Xf51=0.2

 　　　　　　　　　　　　　　 对m2的导数f52=1，反向传递　　      0.2X(1)=f1Xf2Xf3Xf4Xf52=0.2

...

需要注意的是，误差从输出一层一层往前传播，不可以跳过某些中间步骤，在计算每一步的误差时，需要乘上上一步得到的误差（链式法则，层层相乘）。

在传播过程中，如果某一部分可以直接用一整个函数代替，则可以对整块求导，然后将导数值传到上一步，如下图所示，这仍然符合链式求导法则。

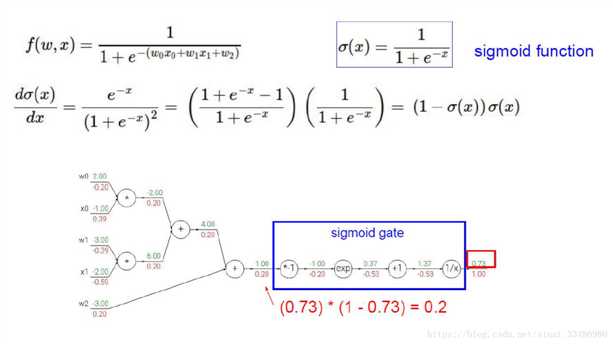
蓝色框内其实就是sigmoid函数，其导数为 f(1-f)=(0.73x(1-0.73))=0.2，反向传递 1X0.2=0.2

其实在实际过程中，完整的反向传播应该是下图

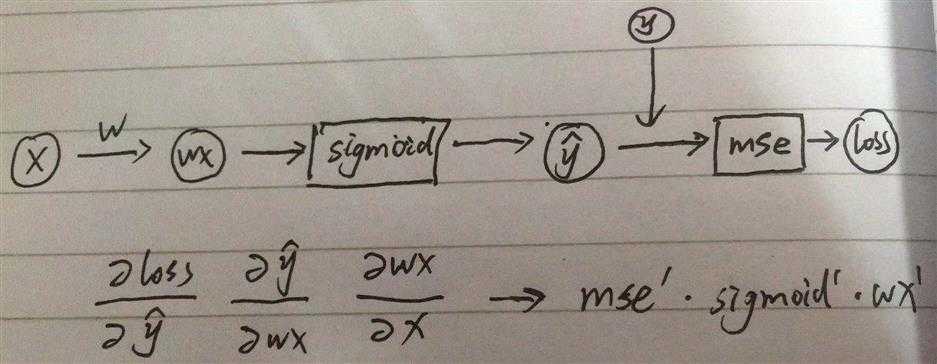
是不是觉得链式法则很有用？

链式法则玩转反向传播

标签：直接   传递   ror   nbsp   com   理解   逻辑回归   跳过   蓝色   

原文地址：https://www.cnblogs.com/yanshw/p/10461330.html