标签：多个参数   nbsp   font   匹配   str   new   因此   元素   最小二乘法   

最小二乘法

一、什么是最小二乘法

最小二乘法作为一种数学优化技术，通过最小化误差的平方和寻找数据的最佳函数匹配。（重点：寻找匹配函数）

以身高体重为例，我们有这样的生活常识，在无系统误差的情况下，身高与体重近似的是一个线性关系，即y=θ₁·x+θ₀。其中y是体重，x是身高。此时，我们就可以用最小二乘法求出θ₁和θ₀

二、代价函数Cost function

根据最小二乘法的定义我们可以看出，所求的最佳函数应该满足误差的平方和最小化，因此不难得出Cost functiond的数学描述为：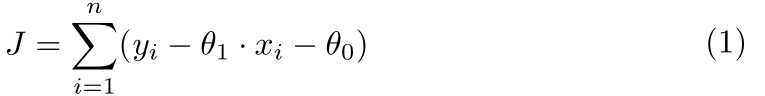

其中θ₁·x+θ₀为估计算出来的值，y_i为真实值。此时，我们的目标就是确定θ₁，θ₀使得Cost function的值最小，于是我们对θ₁，θ₀求偏导并使其等于0，整理即可求出θ₁，θ₀的值。

 三、一般情况下的最小二乘法

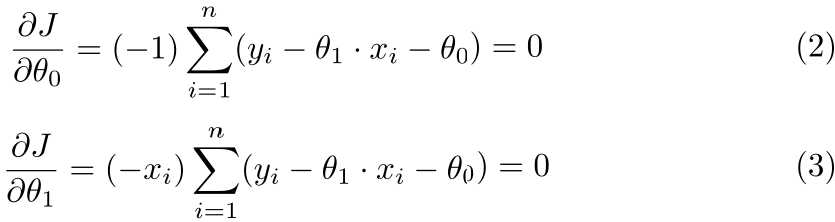
实际情况是，我们的样本集合往往有多个相关变量X=[1,x^₁,x^₂,...,x^_m](考虑到矩阵乘法的实际意义，往往令该向量的第一个元素为1),多个参数θ=[θ₀,θ₁,...,θ_m],则可以推广到如下的线性形式：

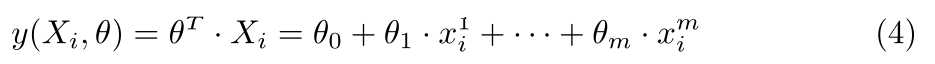
我们令样本矩阵为X，真实值记为Y，则有：

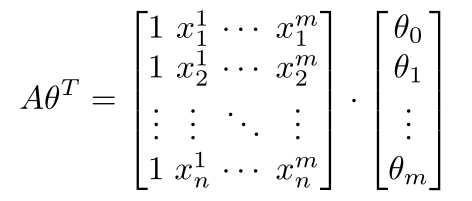
由上面对最小二乘法的讨论我们可以确定我们的目标，即求得最优解θ使得Cost function函数值最小，即：

解得最优解为：

附matlab实例：

数模学习——最小二乘法

标签：多个参数   nbsp   font   匹配   str   new   因此   元素   最小二乘法   

原文地址：https://www.cnblogs.com/wyb6231266/p/10473095.html