标签:tor 结果 max represent 范围 cto 池化层 而且 集中
原文链接:https://yq.aliyun.com/topic/111
在神经网络(甚至深度学习)参数训练中,BP算法占据举足轻重的地位。
实际上BP算法是一个典型的双向算法,但通常强调的是反向传播。
工作流程分两大步:
反向传播演示:https://google-developers.appspot.com/machine-learning/crash-course/backprop-scroll/
会存在“梯度扩散(Gradient Diffusion)”现象,其根源在于对于非凸函数,梯度一旦消失,就没有指导意义,导致它可能限于局部最优。
而且“梯度扩散”现象会随着网络层数增加而愈发严重,也就是说,随着梯度的逐层消减,导致它对调整网络权值的调整效益,作用越来越小。
故此BP算法多用于浅层网络结构(通常小于等于3),这就限制了BP算法的数据表征能力,从而也就限制了BP的性能上限。
在本质上,BP算法是一种全连接神经网络,虽然有很多成功的应用,但只能适用于“浅层”网络。
因为“肤浅”,所以也就限制了它的特征表征能力,进而也就局限了它的应用范围。
当前适用在图像、语音识别等众多任务。
CNN能够直接从原始图像出发,经过非常少的预处理,就能从图像中找出视觉规律,进而完成识别分类任务,其实这就是端到端(end-end)的含义。
避免了对图像进行复杂的前期处理(即大量的人工图像特征提取工作)
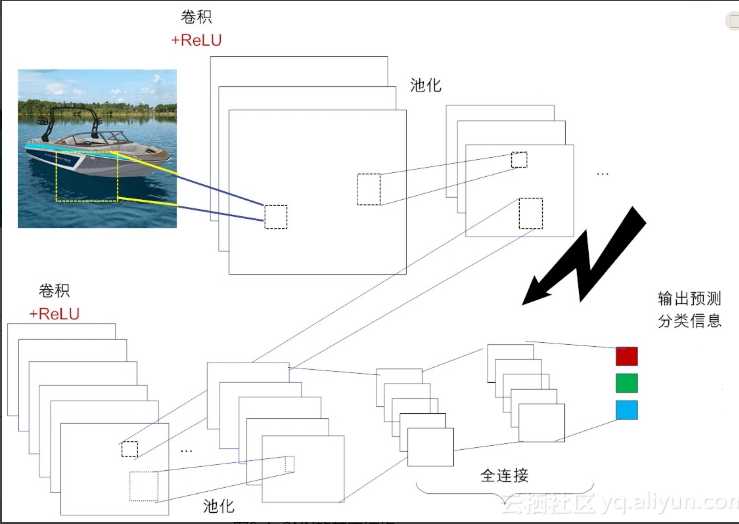
当前主流的卷积神经网络结构,其精华大致体现在3个核心操作和3个概念。
卷积操作的数学意义:一个函数和另一个函数在某个维度上的加权“叠加”作用。
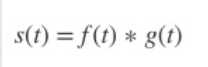
通常把函数f称为输入函数, g 称为滤波器(filter,也称为特征检测器,feature detector)或卷积核(kernel),这两个函数的叠加结果称为特征图或特征图谱(feature map)
特征图谱也被称呼为做卷积特征(convolved feature)或激活图(activation map)。
在本质上,离散卷积就是一个线性运算,因此离散卷积操作也被称为线性滤波。
常用于图像处理的卷积核
同一化核(Identity)
卷积后得到的图像和原图一样。
只有中心点的值是1,邻域点的权值都是0,所以对滤波后的取值没有任何影响。
边缘检测核(Edge Detection)
也称为高斯-拉普拉斯算子。
矩阵的元素总和为0(即中间元素为8,而周围8个元素之和为-8),所以滤波后的图像会很暗,而只有边缘位置是有亮度的。
图像锐化核(Sharpness Filter)
图像的锐化和边缘检测比较相似。
首先找到边缘,然后再把边缘加到原来的图像上面,强化了图像的边缘,使得图像看起来更加锐利。
均值模糊(Box Blur /Averaging)
每个元素值都是1,它将当前像素和它的四邻域的像素一起取平均,然后再除以9。
均值模糊比较简单,但图像处理得不够平滑。因此,还可以采用高斯模糊核(Gaussian Blur),这个核被广泛用在图像降噪上。

相比于全连接的前馈网络,卷积神经网络的结构要简洁,但并不简单。
在不考虑输入层的情况下,一个典型的卷积神经网络通常由若干个卷积层、激活层、池化层及全连接层组成。
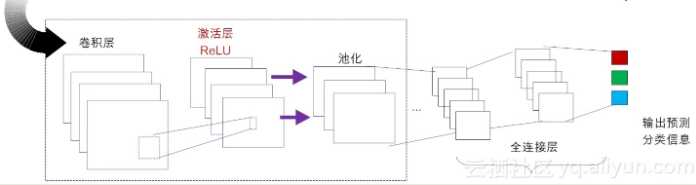
卷积层(Convolutional Layer)
- 是卷积神经网络的核心所在。
- 在卷积层,通过实现“局部感知”和“权值共享”等系列的设计理念,可达到两个重要的目的:对高维输入数据实施降维处理和实现自动提取原始数据的核心特征。激活层(Activation Layer)
- 作用是将前一层的线性输出,通过非线性激活函数处理,从而可模拟任意函数,进而增强网络的表征能力。
- 在深度学习领域,ReLU(Rectified-Linear Unit,修正线性单元)是目前使用较多的激活函数,原因是它收敛更快,且不会产生梯度消失问题。池化层(Pooling Layer)
- 也称为亚采样层(Subsampling Layer)。
- 简单来说,利用局部相关性,“采样”在较少数据规模的同时保留了有用信息。
- 巧妙的采样还具备局部线性转换不变性,从而增强卷积神经网络的泛化处理能力。全连接层(Fully Connected Layer)
相当于传统的多层感知机(Multi-Layer Perceptron,简称MLP)。
通常来说,“卷积-激活-池化”是一个基本的处理栈,通过多个前栈处理之后,待处理的数据特性已有了显著变化:
一方面,输入数据的维度已下降到可用“全连接”网络来处理了;另一方面,此时全连接层的输入数据已不再是“泥沙俱下、鱼龙混杂”,而是经过反复提纯过的结果,因此最后输出的结果要可控得高。可以根据不同的业务需求,构建出不同拓扑结构的卷积神经网络
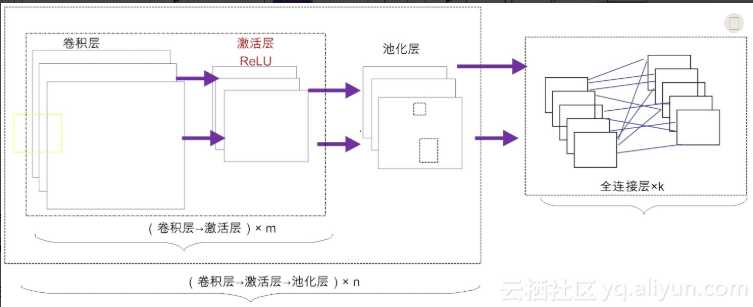
例如,可以先由m个卷积层和激活层叠加,然后(可选)进行一次池化操作,重复这个结构n次,最后叠加k个全连接层(m, n, k ≥ 1)。
总体来讲,卷积神经网络通过多层处理,逐渐将初始的“低层”特征表示,转化为“高层”特征表示,之后再用“简单模型”即可完成复杂的分类等学习任务。
因此在本质上,深度学习就是一个“特征学习(feature learning)”或“表示学习(representation learning)”。
卷积层的三个核心概念:局部连接、空间位置排列及权值共享。
局部连接(Local Connectivity)
全连接的前馈神经网络有个非常致命的缺点,那就是可扩展性(Scalability)非常差。
原因非常简单,网络规模一大,需要调参的个数以神经元数的平方倍增,导致它难以承受参数太多之痛。
局部连接(Local Connectivity)在能某种程度上缓解这个“参数之痛”。
局部连接也被称为“稀疏连接(Sparse Connectivity)”。
对于卷积神经网络而言,隐藏层的神经元仅仅需要与前一层的部分区域相连接。
这个局部连接区域有个特别的名称叫“感知域(receptive field)”,其大小等同于卷积核的大小
。
相比于原来的全连接,连接的数量自然是稀疏得多,因此,局部连接也被称为“稀疏连接(Sparse Connectivity)”。
但需要注意的是,这里的稀疏连接,仅仅是指卷积核的感知域相对于原始图像的高度和宽度而言的。
卷积核的深度(depth,在这里卷积核的深度实际上就是卷积核的个数。)则需要与原始数据保持一致,不能缩减。空间排列(Spatial arrangement)
在构造卷积层时,对于给定的输入数据,如果确定了卷积核的大小,卷积核的深度(个数)、步幅以及补零个数,那么卷积层的空间安排就能确定下来。
也就是说固定4个参数:卷积核的大小、深度、步幅及补零。
卷积核的深度(depth)
卷积核的深度对应的是卷积核的个数。每个卷积核只能提取输入数据的部分特征。
每一个卷积核与原始输入数据执行卷积操作,会得到一个卷积特征,这样的多个特征汇集在一起,称为特征图谱。
事实上,每个卷积核提取的特征都有各自的侧重点。
因此,通常说来,多个卷积核的叠加效果要比单个卷积核的分类效果要好得多。
步幅(stride)
即滤波矩阵在输入矩阵上滑动跨越的单元个数。
设步幅大小为S,当S为1时,滤波器每次移动一个像素的位置。
当S为2时,每次移动滤波器会跳过2个像素。S越大,卷积得到特征图就越小。
补零(zero-padding)
补零操作通常用于边界处理。
在有些场景下,卷积核的大小并不一定刚好就被输入数据矩阵的维度大小整除,就会出现卷积核不能完全覆盖边界元素的情况。
这时,就需要在输入矩阵的边缘使用零值进行填充,使得在输入矩阵的边界处的大小刚好和卷积核大小匹配。
这样做的结果,相当于对输入图像矩阵的边缘进行了一次滤波。
零填充的好处在于,它可以控制特征图的大小。
使用零填充的卷积叫做泛卷积(wide convolution),不适用零填充的叫做严格卷积(narrow convolution)。
权值共享(Shared Weights)
权值实际上就是不同神经元之间的连接参数,也称为参数共享(Parameter Sharing)。
局部连接虽然降低了连接的个数,但整体幅度并不大,需要调节的参数个数依然非常庞大,因此还是无法满足高效训练参数的需求。
而权值共享能显著降低参数的数量。
对于同一个卷积核,它在一个区域提取到的特征,也能适用于于其他区域。
基于权值共享策略,将卷积层神经元与输入数据相连,同属于一个特征图谱的神经元,将共用一个权值参数矩阵。
权值共享保证了在卷积时只需要学习一个参数集合即可,而不是对每个位置都再学习一个单独的参数集合。
因此参数共享也被称为绑定的权值(tied weights)。空间位置排列确定了神经网络的结构参数,而局部连接和权值共享等策略显著降低了神经元之间的连接数。
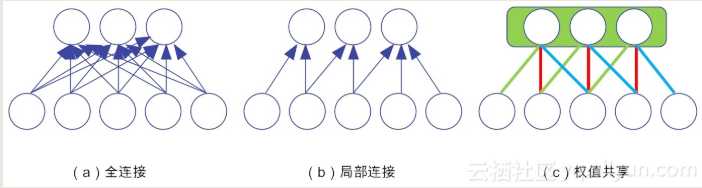
示例:全连接(不包括偏置的权值连接)的参数为15个,局部连接为7个,而权值共享的参数为3个(即红绿蓝线分别共用一个参数)
欠拟合(underfitting)
样本不够,或学习算法不精,连已有数据中的特征都没有学习好,自然当面对新样本做预测时,效果肯定也好不到哪里去。
欠拟合比较容易克服,比如在神经网络中增加训练的轮数,从而可以更加“细腻”地学习样本种的特征。
过拟合(overfitting)
构建的模型一丝不苟地反映已知的所有数据,但这样一来,它对未知数据(新样本)的预测能力就会比较差。
卷积神经网络如何泛化(即防过拟合)
采样(sampling)
采样的本质就是力图以合理的方式“以偏概全”。
在卷积神经网络中,采样是针对若干个相邻的神经元而言的,因此也称为“亚采样(Subsampling)”,也就是“池化(Pooling)”。激活层存在的最大目的,莫过于引入非线性因素(选取合适的“激活函数”),以增加整个网络的表征能力。
Sigmoid激活函数的缺点
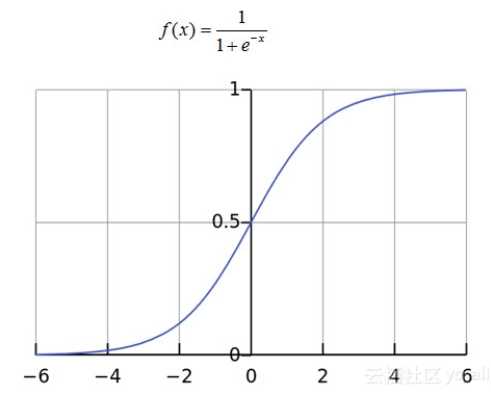
导数值很小。比如说,Sigmoid的导数取值范围仅为[0, 1/4],且当输入数据很大或者很小的时候,其导数趋都近于0。
这就意味着,很容易产生所谓的梯度消失(vanishing gradient)现象。激活函数修正线性单元(Rectified Linear Unit,简称ReLU)
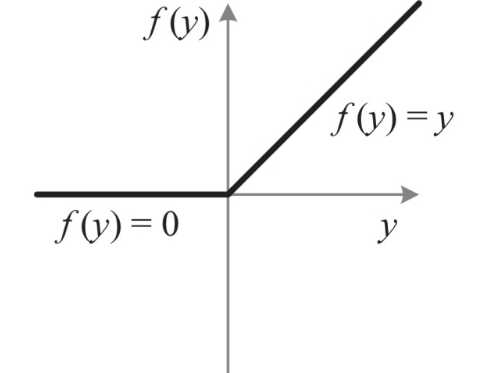
标准的ReLU函数为f(x)=max(x,0),即当x>0时,输出x; 当x<=0时,输出0。
相比于Sigmoid类激活函数,ReLU激活函数的优点
- 单侧抑制。当输入小于0时,神经元处于抑制状态。反之,当输入大于0,神经元处于激活状态。
- 相对宽阔的兴奋边界。Sigmoid的激活态(即f(x)的取值)集中在中间的狭小空间,而ReLU这不同,只要输入大于0,神经元一直都处于激活状态。
- 稀疏激活性。ReLU直接把抑制态的神经元“简单粗暴”地设置为0,就使得这些神经元不再参与后续的计算,从而造成网络的稀疏性,
ReLU激活函数除了减少了计算量,还减少了参数的相互依存关系(网络瘦身了不少),使其收敛速度远远快于其他激活函数,最后还在一定程度上缓解了过拟合问题的发生。
LeRU的这种简单直接的处理方式,也带来一些副作用。
最突出的问题就是,会导致网络在训练后期表现得非常脆弱,以至于这时的ReLU也被戏称为“死掉的ReLU(dying ReLU)”。标签:tor 结果 max represent 范围 cto 池化层 而且 集中
原文地址:https://www.cnblogs.com/anliven/p/6285378.html