标签:ali not mis info mamicode reply NPU eterm cin
线段树是用来对一堆数据处理的树结构,它的核心思想是二分(一般都用递归实现)。
树里需要存的是编号,和区间的左右,还有就是看题目需要了
二叉树特性:1:左子树编号是父树的2倍,右子树是父树的2倍加一 。
2:左子树l是父树的l,左子树的r是父树的(l+r)/2;右子树的l是父树的(l+r)/2 +1,右子树的r是父树的r
如图:
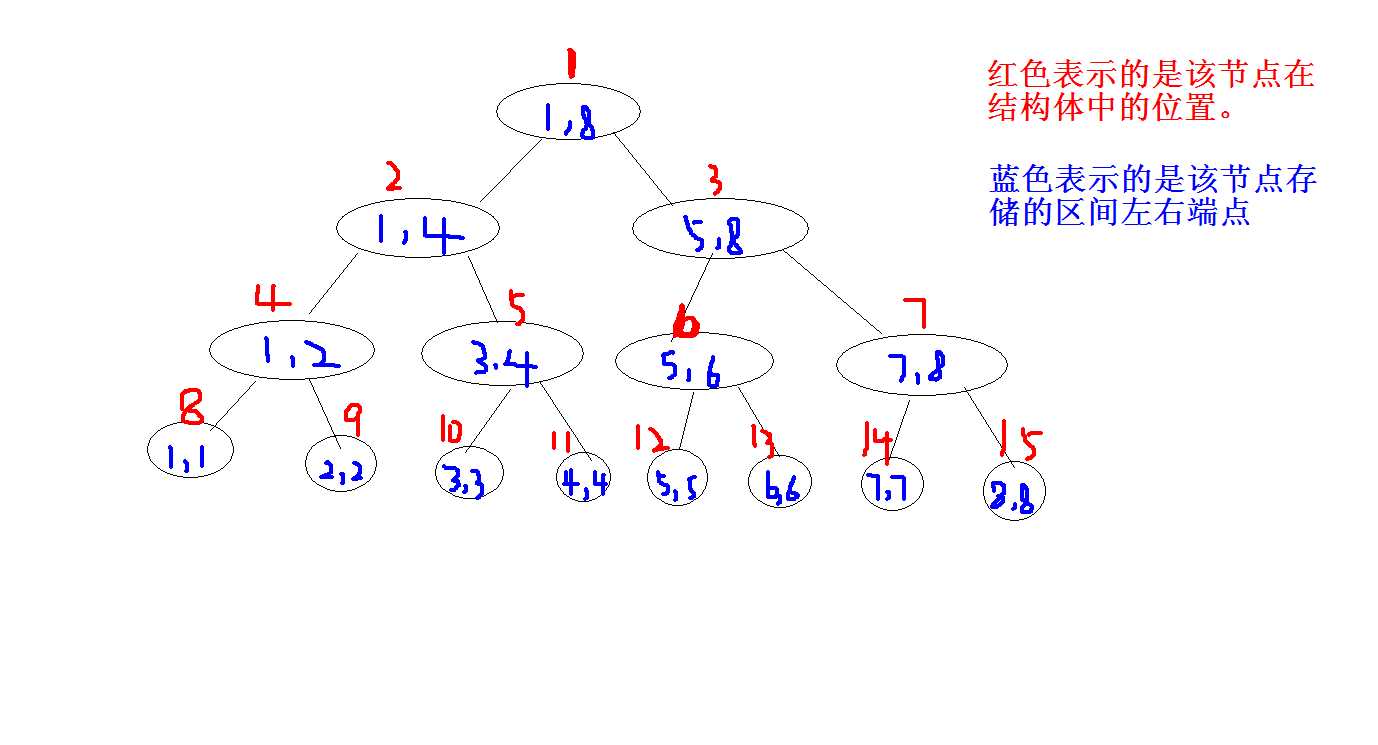
图是偷来的,推荐那个大佬的博客吧:http://www.cnblogs.com/TheRoadToTheGold/p/6254255.html
初学者一般都是从用它来计算给定一组有序数列(数据量一般都超级大),然后问你某个区间的值(是不是觉得用前缀和就可以写?但是他还有另外一个条件),而且在询问你的过程中,他还可以对序列中的数进行更改,再接着询问你某个区间的和。(现在应该不能用前缀和写了吧,毕竟数据量一大,它改了某个点的值,那你就要改与这个点有关的和全部改变)。这时候,你就可以用线段树来写,它是将区间二分,是一个完整的二叉树。
看代码吧。

1 #include<iostream> 2 #include<cstdio> 3 #define Maxn 50010 4 using namespace std; 5 int kp; 6 //:树 7 struct Tree{ 8 int l;//(l,r) 9 int r; 10 int sum;//(l,r)上的和 11 }tree[Maxn]; 12 //1:建树 13 //:树特性:1:左子树编号是父树的2倍,右子树是父树的2倍加一 。 14 //2:左子树l是父树的l,左子树的r是父树的(l+r)/2;右子树的l是父树的(l+r)/2 +1,右子树的r是父树的r 15 void Btree(int k,int l,int r)//k:节点编号,l:左,r:右 16 { 17 tree[k].l=l,tree[k].r=r; 18 if(l==r){ 19 scanf("%d",&kp); 20 tree[k].sum=kp; 21 return ; 22 } 23 int mid=(l+r)/2; 24 Btree(k*2,l,mid); 25 Btree(k*2+1,mid+1,r); 26 tree[k].sum=tree[k*2].sum+tree[k*2+1].sum; 27 } 28 //查询 29 int ans=0; 30 void query(int k,int l,int r,int start,int ed){//要查询的区间 (start,ed) 31 32 if(start<=l&&ed>=r){ 33 ans+=tree[k].sum; 34 return ; 35 } 36 37 //考虑左走还是右走,还是左右都走 38 int mid=(l+r)/2; 39 if(ed<=mid){//左 40 query(k*2,l,mid,start,ed); 41 42 }else if(start>=mid+1){//右 43 query(k*2+1,mid+1,r,start,ed); 44 45 }else{//左加右 46 query(k*2,l,mid,start,ed); 47 query(k*2+1,mid+1,r,start,ed); 48 49 } 50 return ; 51 } 52 53 //更改 54 void change(int k,int l,int r,int aim,int val){//aim更改的元素下标 ,val是把aim元素更改为val 55 56 if(l==r&&aim==l){ 57 tree[k].sum=val; 58 return ; 59 } 60 int mid=(l+r)/2; 61 if(aim>=l&&aim<=mid){//l,r要一直逼近aim==l,aim==r 62 change(k*2,l,mid,aim,val); 63 64 }else{ 65 change(k*2+1,mid+1,r,aim,val); 66 67 } 68 69 tree[k].sum=tree[k*2].sum+tree[k*2+1].sum;//回溯时改变值 70 } 71 int main(){ 72 int n,k=1; 73 cin>>n; 74 Btree(1,1,n);//建立一个根节点区间是【1,n】的树 75 //**********演示***************** 76 for(int i=1;i<=7;i++){ 77 cout<<" ("<<tree[i].l<<" , "<<tree[i].r<<") "<<tree[i].sum<<endl; 78 } 79 query(1,1,n,1,3);//询问 80 cout<<ans<<endl; 81 ans=0; 82 change(1,1,n,1,100);//改变一个值 83 for(int i=1;i<=7;i++){ 84 cout<<" ("<<tree[i].l<<" , "<<tree[i].r<<") "<<tree[i].sum<<endl; 85 } 86 query(1,1,n,1,3);//再次询问 87 cout<<ans<<endl; 88 return 0; 89 }
输出:

poj3246
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions:68003 | Accepted: 31585 | |
| Case Time Limit: 2000MS | ||
Description
For the daily milking, Farmer John‘s N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things simple, he will take a contiguous range of cows from the milking lineup to play the game. However, for all the cows to have fun they should not differ too much in height.
Farmer John has made a list of Q (1 ≤ Q ≤ 200,000) potential groups of cows and their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to determine the difference in height between the shortest and the tallest cow in the group.
Input
Output
Sample Input
6 3 1 7 3 4 2 5 1 5 4 6 2 2
Sample Output
6 3 0
Source
思路:它只需将前面存和改成存最大最小值即可
代码:

1 #include<iostream> 2 #include<cstdio> 3 #define Maxn 50010 4 using namespace std; 5 int kp; 6 //:树 7 struct Tree{ 8 int l;//(l,r) 9 int r; 10 int sum;//(l,r)上的和 11 int minn,maxx; 12 }tree[Maxn*4];//因为是树,所以它是比题目给的点的数据最大还要大,开4倍就一定够 13 //1:建树 14 //:树特性:1:左子树编号是父树的2倍,右子树是父树的2倍加一 。 15 //2:左子树l是父树的l,左子树的r是父树的(l+r)/2;右子树的l是父树的(l+r)/2 +1,右子树的r是父树的r 16 void Btree(int k,int l,int r)//k:节点编号,l:左,r:右 17 { 18 tree[k].l=l,tree[k].r=r; 19 if(l==r){ 20 scanf("%d",&kp); 21 tree[k].maxx=tree[k].minn=kp; 22 return ; 23 } 24 int mid=(l+r)/2; 25 Btree(k*2,l,mid); 26 Btree(k*2+1,mid+1,r); 27 tree[k].maxx=max(tree[k*2].maxx,tree[k*2+1].maxx); 28 tree[k].minn=min(tree[k*2].minn,tree[k*2+1].minn); 29 } 30 //查询 31 int Max,Min; 32 void query(int k,int l,int r,int start,int ed){//要查询的区间 (start,ed) 33 34 if(start<=l&&ed>=r){ 35 Max=max(tree[k].maxx,Max); 36 Min=min(tree[k].minn,Min); 37 return ; 38 } 39 40 //考虑左走还是右走,还是左右都走 41 int mid=(l+r)/2; 42 if(ed<=mid){//左 43 query(k*2,l,mid,start,ed); 44 45 }else if(start>=mid+1){//右 46 query(k*2+1,mid+1,r,start,ed); 47 48 }else{//左加右 49 query(k*2,l,mid,start,ed); 50 query(k*2+1,mid+1,r,start,ed); 51 52 } 53 return ; 54 } 55 56 //更改 57 void change(int k,int l,int r,int aim,int val){//aim更改的元素下标 ,val是把aim元素更改为val 58 59 if(l==r&&aim==l){ 60 tree[k].sum=val; 61 return ; 62 } 63 int mid=(l+r)/2; 64 if(aim>=l&&aim<=mid){//l,r要一直逼近aim==l,aim==r 65 change(k*2,l,mid,aim,val); 66 67 }else{ 68 change(k*2+1,mid+1,r,aim,val); 69 70 } 71 72 tree[k].maxx=max(tree[k*2].maxx,tree[k*2+1].maxx); 73 tree[k].minn=min(tree[k*2].minn,tree[k*2+1].minn); 74 } 75 int main(){ 76 int n,q; 77 int l,r; 78 cin>>n>>q; 79 Btree(1,1,n); 80 while(q--){ 81 scanf("%d%d",&l,&r); 82 Max=-1,Min=0x3f3f3f3f; 83 query(1,1,n,l,r); 84 printf("%d\n",Max-Min); 85 } 86 return 0; 87 }
标签:ali not mis info mamicode reply NPU eterm cin
原文地址:https://www.cnblogs.com/liuzuolin/p/10490900.html